非球面、自由曲面的优化及公差分析一直是光学设计中的难点，如果考虑到加工及装配，情况会变得更加复杂。

球面、圆锥曲面、偶次非球面的优化及公差分析相对更加成熟一些，ZEMAX里边可以直接支持；然而，其他的一些非球面类型如Q型非球面、泽尼克面型、扩展多项式面型、切比雪夫面型使用的过程中需要格外的小心，尤其是公差分析方面。

球面、圆锥曲面、偶次非球面的优化及公差分析相对更加成熟一些，ZEMAX里边可以直接支持；然而，其他的一些非球面类型如Q型非球面、泽尼克面型、扩展多项式面型、切比雪夫面型使用的过程中需要格外的小心，尤其是公差分析方面。

核心功能点：

1. 支持Qbfs公差分析：面型精度RMS值或者斜率公差（影响干涉仪检测的难易度、精度）

2. 支持Qcon公差分析：面型精度RMS值

3. 支持泽尼克面型公差分析：面型精度RMS值

4. 支持泽尼克面型向扩展多项式面型（Extended Polynomial）的转化，方便加工及制图

5. 优化的时候可以控制泽尼克面型的偏移及旋转，保证加工及检测精度

一：如何对Q型非球面进行公差分析？
Q型非球面分为两大类：

A. Qbfs: 偏离”最佳拟合”球面的Q型非球面

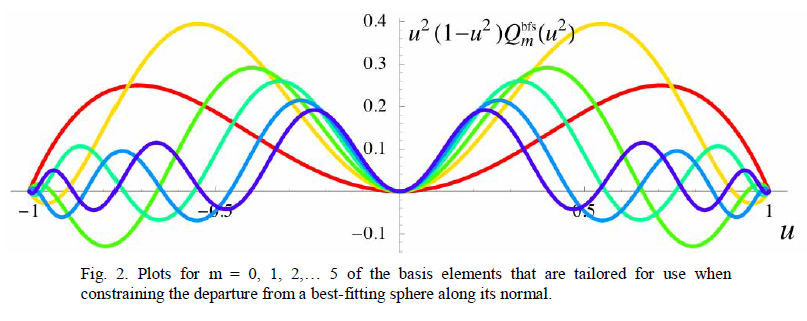
B. Qcon: 偏离相对应圆锥曲面的Q型非球面

ZEMAX里边目前不能直接支持对这类Q型非球面的公差分析，比较常见的做法，就是直接对非球面系数通过TPAR公差操作数的形式进行公差分析，然而此方法的意义比较模糊，虽然这些系数与加工、测试有一定的相关性，可以大致定性的判断，然而无法严格定量化的分析。

对于Qbfs: 我们定义均方根斜率偏差Krms：可以表征干涉仪全孔径测量的可行性

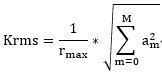
r_max为非球面最大半口径，a_m为Qbfs非球面系数， Krms表征与最接近球面的法向偏离, 该值越小越容易测量及加工。

干涉仪测量已经成为公认的业内测量标准：高精度、全口径测量。但干涉仪的测量条件相对苛刻，只能测量比较缓和的非球面，非球面度非常大的情形，需要加一些额外的补偿条件，成本极高。对于比较缓和的非球面（偏离球面比较小），可以用一般的干涉仪进行全孔径测量，而且精度很高，而无需额外并且昂贵的补偿镜（Null Lens）、计算全息补偿（CGH），极大的节省检测成本及时间周期。

然而设计上，经常用偶次非球面作为非球面设计的首选，一方面由于其表达相对简单，另一方面可能由于加工设备的原因；但从检测上讲，尤其是精度要求比较高的场合，偶次非球面并不是一个非常理想的面型。

对于一个具有NXN像元，波长为λ的激光干涉仪，在奈奎斯特采样频率，其要求

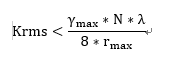
γ_max为最大的可接受均方根光圈密度（RMS Fringe Density）。

因此我们可以将Krms作为约束引入到优化当中，或者将其作为公差变动量引入到面型公差分析中去。

应用1：在激光应用中，我们可能经常用到激光的准直及聚焦，透镜的加工质量直接影响到激光的光束质量，在一些对激光质量要求比较高的场合，需要设计一符合加工及干涉仪检测要求的高质量非球面透镜，成本越低，周期越短越好。

假设常规干涉仪的波长为0.6328um，像元数目为1KX1K,全口径检测无需任何的补偿镜，要求：Krms<0.001.

用常规的偶次非球面设计：

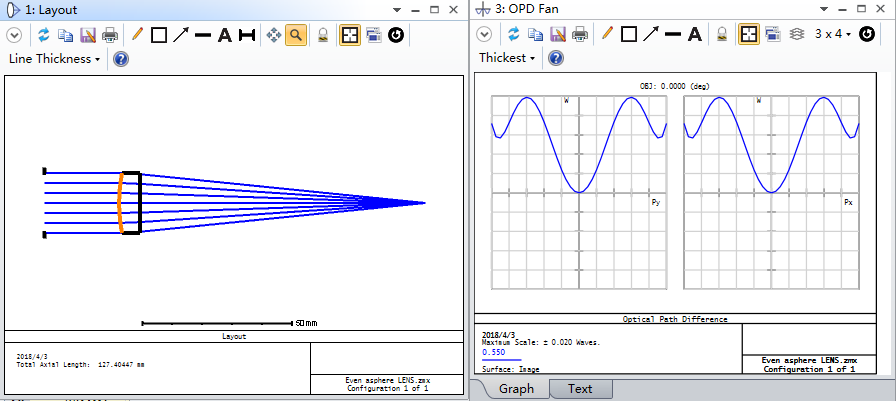
用我们的Zernike_Qtype模块，施加Krms约束（<0.001）进行的优化

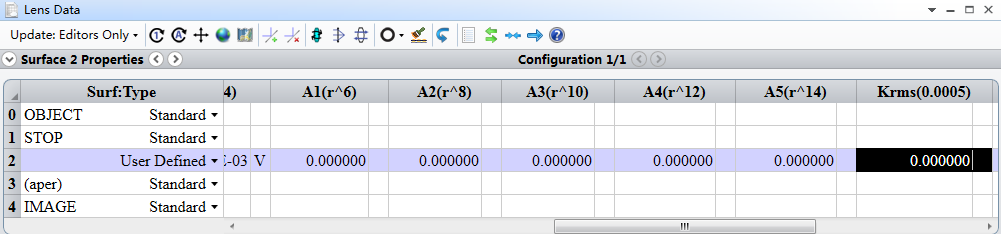
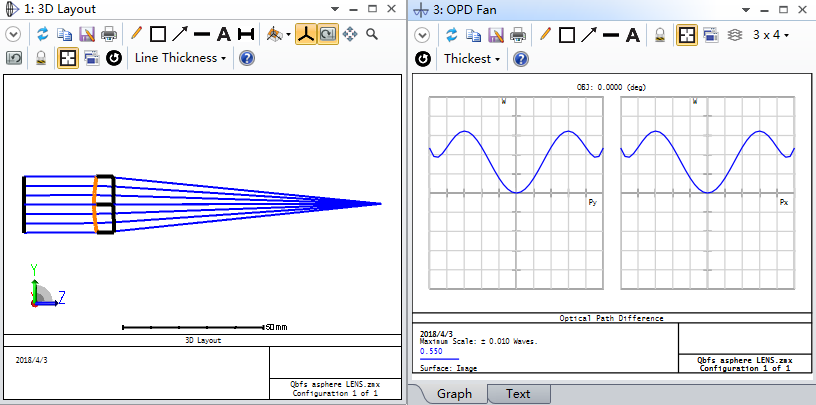
对比的结果：

因此我们可以直接设计出易于测量及加工的非球面形式，能够极大的保证检测精度及节省成本；如果采用偶次非球面形式，检测及加工的精度很难直接去判定，有可能导致检测的成本极高。

应用2：对Q型非球面面型进行公差分析

对Qbfs:我们可以施加rms斜率偏差（Krms）或者RMS矢高偏差
对Qcon:我们可以施加rms矢高偏差，这是因为Qcon一般表征的是大非球面度的非球面，
这类非球面干涉仪直接测量几乎不太现实，一般用如轮廓仪进行矢高测量。

a：对例1的结果进行Krms公差分析

我们通过TPAR对Krms施加1E-4的斜率公差，运行200次蒙特卡洛结果，以RMS波前差作为判据。未作公差前，系统的RMS波前差为0.00089763.运行后可以看到波前差的概率分布如下表所示：

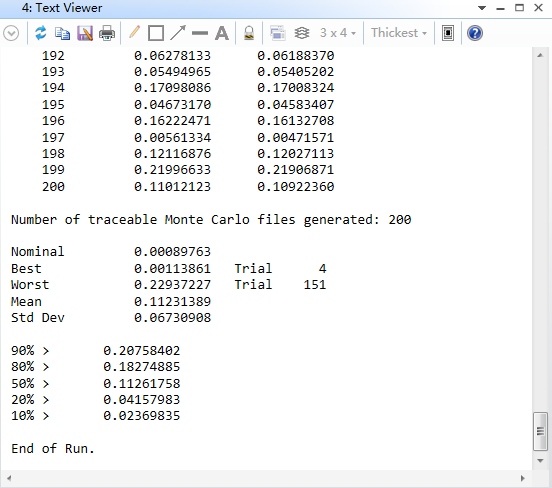
b: 对例1的结果进行RMS矢高公差分析，我们采用Zernike的形式来表征矢高偏离，只采用Z4-Z7项，同样可以用TPAR公差操作数来指定，假设施加0.2um的RMS矢高偏离，来看波前差的变化;未作矢高公差之前，系统的RMS波前差为0.00089763。

运行蒙特卡洛公差分析之后：系统RMS波前的概率分布如下

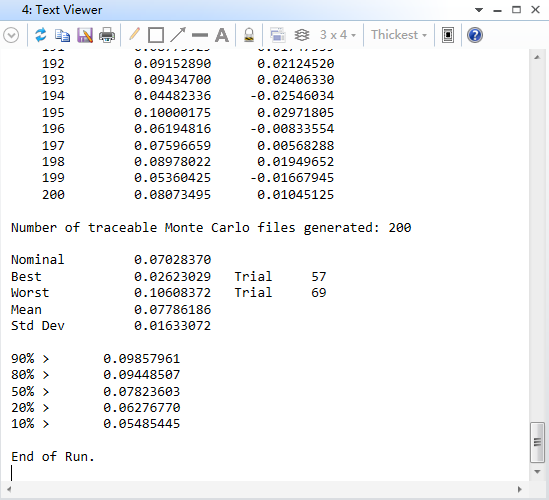
二：Zernike_Qtype模块的另一功能是可以对泽尼克自由曲面设计进行公差分析，目前针对泽尼克面型Zemax里边没有直接的方法进行公差分析。

对泽尼克面型我们在做公差分析的时候，也是通过施加RMS矢高偏差来实现面型的公差分析，有点类似应用2(b)的案例，施加的不规则度面型结果如下：在此不再熬述

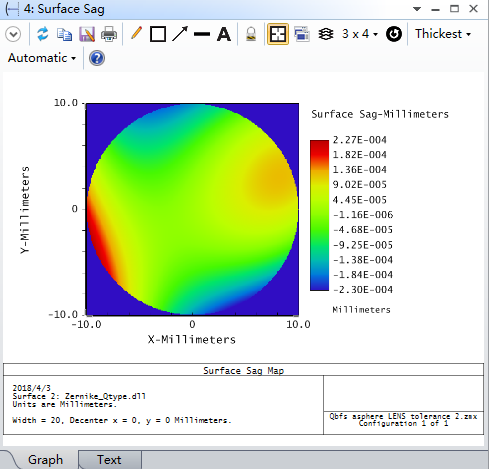
三：利用Zernike_Qtype模块对泽尼克面型进行转化，转化为扩展多项式面型（Extended Polynomial surface）。如果你的供应商不支持泽尼克自由曲面的加工，我们可以将其转化为更常用的扩展多项式面型，并且可以更容易的进行制图、出图。

转化前后的比较：

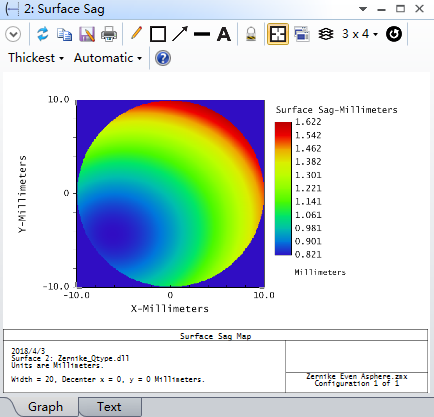
转化之前（Zernike面型）

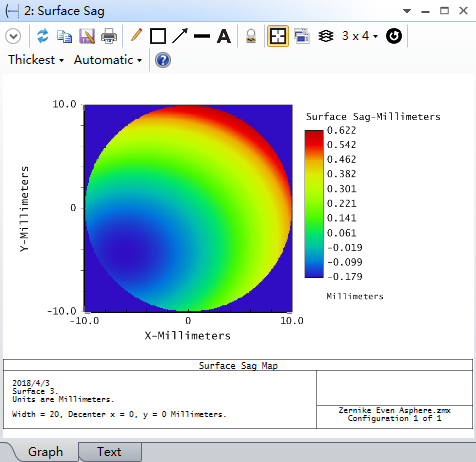
转化之后（扩展多项式面型）

从转化的面型形状及光斑半径可以看到转化的精度很高，几乎是无损失保真变换；细心的朋友可能会注意到面型的峰值及谷值有差别（虽然峰-谷PV值一致），实际上这是泽尼克面型本身携带的平移引起的，在转化后，平移项已经被移除了（实际上转化为了前表面的厚度）， 平移与旋转项是泽尼克的优点也是缺点，最大的缺点是在给供应商提供图纸并标注的时候， 泽尼克自身的参考面与供应商的加工基准面、装配基准面不一致，你在标注的时候很痛苦，供应商在加工的过程中更痛苦，这他妈的啥性质啊。

Ok,我们的Zernike_Qtype模块可以将面型的参考点移动到面型本身上，消除平移的影响，图纸及加工的标注更方便，矢高表达也更容易理解。

转化后的另一个大的优点是：可以通过我们的Tolerance_General.dll（或者以前的ExtendedPolynomial_TE.dll）公差分析模块对该自由曲面进行更全面的公差分析；虽然Zernike_Qtype模块自带有面型公差分析功能（RMS矢高不规则度），但不能对自由曲面的频率（积分长度）、斜率公差、PV面型公差、离轴公差敏感性等进行公差分析，如果要对这些因素进行公差分析，需要借助我们上述的公差分析模块。

关于更详细的自由曲面、非球面公差分析，可以咨询我们。

四： 对泽尼克面型进行优化的时候，可以控制泽尼克的平移及旋转特性

泽尼克面型除了常用于像质、公差等的表征外，另外一个重要应用则是利用其正交性， 对自由曲面进行优化，其比扩展多项式面型、切比雪夫面型更容易控制面型的平滑特性，尤其是边缘的收敛特性，但缺点是旋转对称特性，在要求一些XY对称的场合，其 极坐标的形式不太尽如人意（这时可以参考我们的Freeform_OPT优化模块）。

泽尼克虽然容易控制面型的平滑特性（面型不跑飞），但最大的缺点是会引入平移及旋转，平移在（三）中的例子已经体现出来了，平移及旋转会让设计的参考基准面与加工、装配的基准面不一致，图纸及加工上令供应商很头大，相应的加工、装配、测量误差都会带来很大的不确定度。

针对该情形有两种处理方法：

1. 在优化的时候，就控制泽尼克本身的平移及旋转，使他们为0；光学系统的平移及旋转都通过坐标断点面（Coordinate Break Surface）来实现。这个可以利用我们的Zernike_Qtype模块来实现，Zemax、Code V软件自带的泽尼克面型无法实现该操作。

2. 在优化的时候，不去刻意的控制泽尼克的平移及旋转，但优化完之后，需要把平移及旋转转化为坐标断点面的平移及旋转。目前Zemax，Code V等软件应该没有此项功能，但 我们的”逆向工程模块”可以实现该功能。详情可以关注我们的”逆向工程模块及服务”。