SYNOPSYS光学设计软件|ASAP光学设计软件|SOLIDWORKS 三维建模设计软件|RP Fiber Power仿真设计软件|武汉墨光科技有限公司

解决方案

用 ContourPlot3D 绘制多面体

之前的文章里我们用参数方程的形式探索了环面及其各种变形如环面纽结等等。曲面除了可以用参数方程的形式表示之外，还可以用隐函数的形式表达，即表示为 F(x, y, z) = 0 的解。这种曲面又称之为等值曲面，因为曲面上的每个点都满足 F(x, y, z) = 0 这一条件。Mathematica 提供了绘制等值曲面的函数 ContourPlot3D。不过在这篇文章里，我们并不用它来绘制各种婀娜多姿的曲面，而是尝试用它探索、绘制一些"多面体"。

从最简单的开始

球面

让我们从最简单的，大家耳熟能详的球面方程开始：

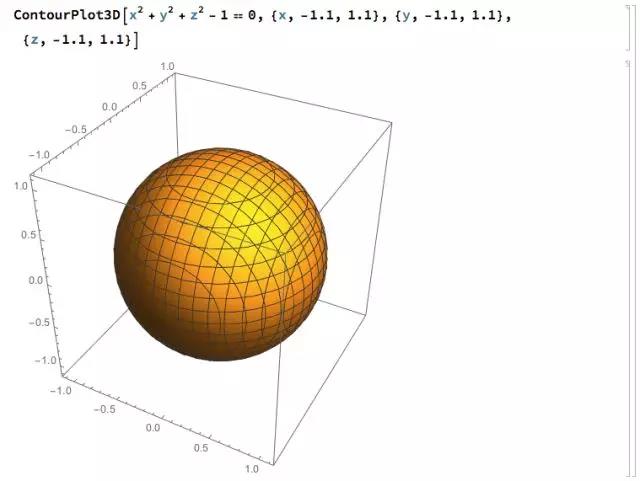
方程 x^2+y^2+z^2==1 的意义非常简单：每个点到原点的距离都是 1，这就形成了一个球面。相比较之下，球面的参数方程就不是这么简单了：

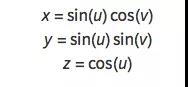
参数方程虽然复杂，但对于计算机程序来说，反而容易绘图，因为根据参数，能直接算出点。而根据方程 F(x, y, z) = 0 计算出满足条件的点就比较困难了，计算时间会比根据参数方程计算要长。

多面体

从球面方程出发，我们可以看一下更一般的形式，比如 x^n+y^n+z^n==1 的图形是什么样子的：

可以看到随着 n 的值不断增大，方程表示的曲面越来越接近一个立方体。这是为什么呢？我并不能完全解释，只能提出这么一个猜测。考虑如下表达式

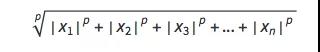
这是 Lp 范数的定义，当 p 趋向于正无穷时，上述表达式的极限是：

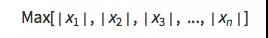
也就是 n 个绝对值中的最大值。把这个结论放到我们的方程 x^n+y^n+z^n==1 上，当 n 不断变大时，在不同方向上就不断接近 | x | == 1、| y | == 1、| z | == 1 三个方程，而这三个方程恰恰是立方体的六个面：x = ±1、y= ±1、z= ±1。根据这个猜测，我们只要能知道多面体各个面的平面方程，就能类比的求得类似上述立方体的“多面体渐近方程”。更进一步的，多面体各个面的平面方程，只要知道面法向量就可以确定平面方程了，如果面法向量是 (a, b, c)，则成对的平面方程就是 a x+b y+ c z = ±1。利用 PolyhedronData 可定义求各种多面体法向量的函数如下：

接下来就让我们用实际计算来验证一下这个猜测吧：

1.正八面体

求正八面体的法向量：

化简并去除方向刚好相反的法向量，因为之前方程的常数项 ±1 可以由一个法向量得到两个相对的面的方程:

然后就可以根据这个求八面体渐近方程了：

2.正十二面体

正十二面体的法向量：

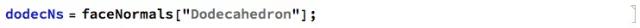
化简并去除方向刚好相反的：

隐函数表达式：

为了计算方便，我们用数值近似取代根号形式：

绘制图形，可以看到，随着次数 n 的不断升高，图形越来越接近正十二面体：

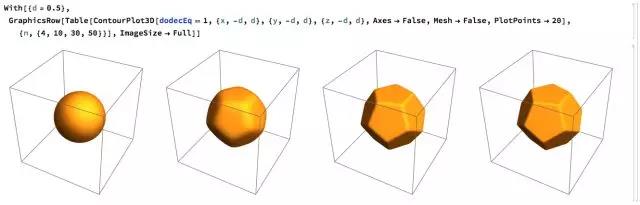
3.十二面体

计算各个面的法向量：

化简并去除方向相反的：

得到方程左侧表达式：

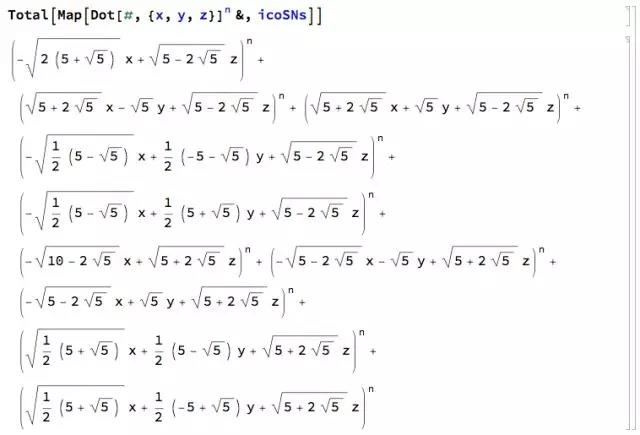
为了计算方便，取近似值：

绘制正二十面体的曲面方程：

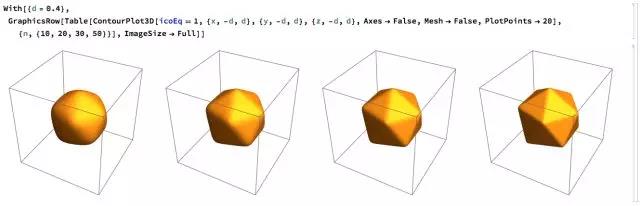
复合多面体

从上面的计算可以看到，根据猜测做的推论基本上是对的：确实据此得到了各种正多面体的渐近方程并成功绘制了出来。但同时也可以看到，这种方法有很多局限性。首先，所生成的多面体必须有平行的相对的面，这样采用的法向量才能一个顶俩，发挥应有的作用得到对应的多面体。五种正多面体里，只有四种满足这个条件，还剩下一个正四面体不能用这种方法表示。其次，用这种方法只能表示凸多面体，所谓凸多面体，就是内部任意两点的连线仍然落在内部的多面体。这两个问题都是可以解决的，解决方法是引入指数函数。

1.正四面体

计算正四面体的法向量：

化简：

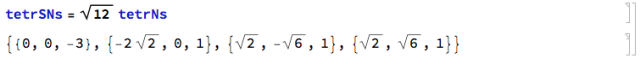
如果用之前的高次方程的方法，那么只能得到一个朝向比较特别的正八面体，因为每个法向量都生成了两个平面：

而改用指数，则可得到如下表达式：

以此作为隐函数果然可以画出正四面体：

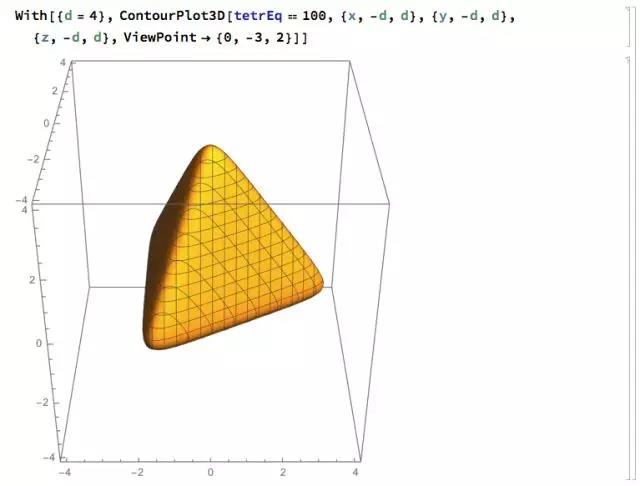
为什么这样可行？我也只能给个近似的猜测：对 E^(a x + by + c z)==C 这样的方程，两边取对数就是 a x+ b y+ c z==log C 这就是一个平面的方程，把几个这样的平面方程加起来，就"围成"了一个多面体。而指数的增长保证了每个方向上不会受其它项的影响，保持大体是个平面。

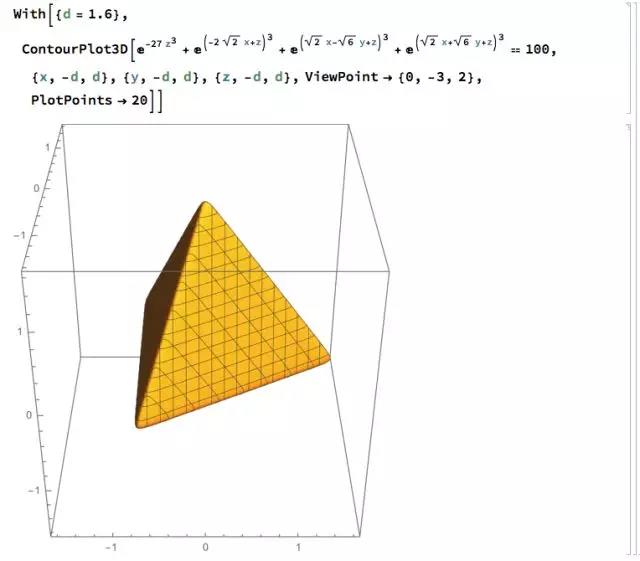
另外还值得指出的是，可以在指数上再加次数，让这样生成的多面体的边缘更加"锐利"：

2.星形

在各种各样的多面体中，有一类多面体可以看作是若干基本的多面体彼此叠合组成，我们称之为复合多面体。比如下图所示的星形八面体，就可以看作两个正四面体彼此叠合而成。

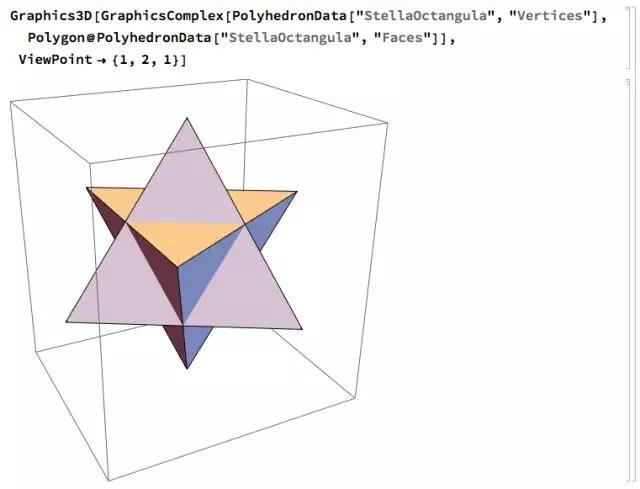
观察这个复合多面体的面的组成指标可以发现，前四组只包含顶点 2、4、5、8，后四组只包含顶点 1、3、6、7。这恰好是各自组成两个正四面体。我们可以照样算出这八个面的法向量，然后分组各自生成两个正四面体曲面：

求法向量，化简并分组：

得到两个指数和的表达式：

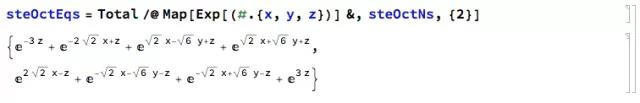
分别绘制可以看到两个正四面体

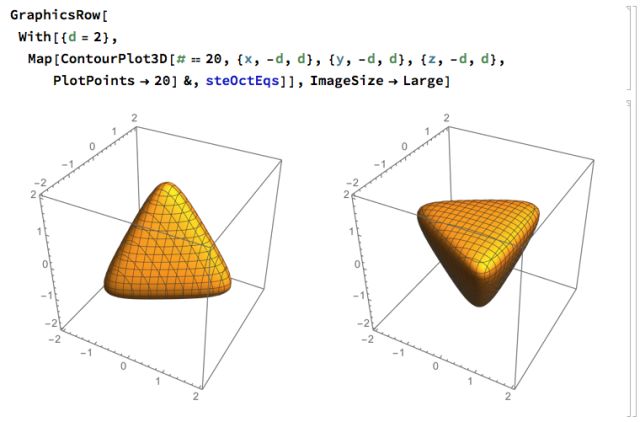
如何从这两个四面体得到想要的星形八面体呢？直接相加肯定是不行的，那样得到的就是正八面体了。这里我们采用 The Nature of Mathematics and the Mathematics of Nature 一书中提到的一个小技巧：把两个方程表达式再次放到指数上。这个技巧称为 Exponential Scale：

可以看到，这个方程确实可以绘制出星形八面体：

可以把旋转观察这个星形八面体曲面的过程输出为动画：

3.五复合正四面体

我们可以再举一个例子，五复合正四面体，这是由五个正四面体内接于一个正十二面体形成的复合多面体：

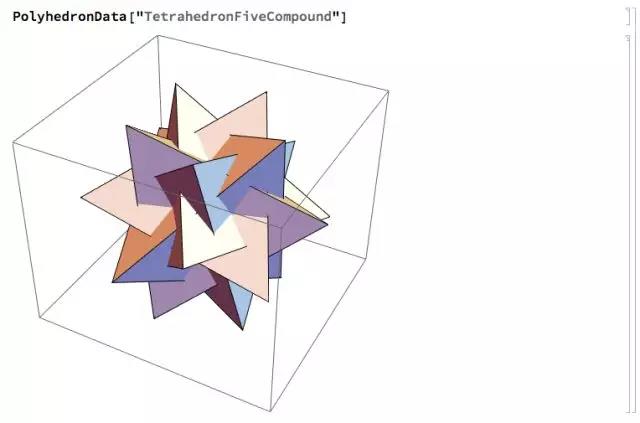
照例求面法向量，化简并分组：

得到方程：

绘制可以得到五复合正四面体的近似曲面（警告：由于项数太多，运行绘制速度很慢，运行时请耐心等待）：

我们也用它生成一个旋转观察的动图：

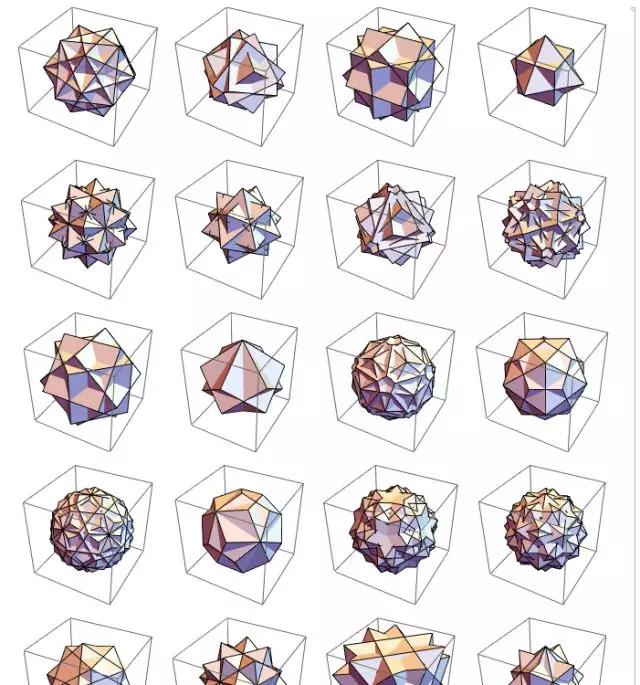
更多的复合多面体

只要是由凸多面体组成的复合多面体，理论上都可以用上面的方法，先求得各个多面体的方程，然后“抬升”到指数位置，得到复合多面体的方程。Mathematica 提供的PolyhedronData 函数里有许多复合多面体，我全部列在下面，感兴趣的读者可以自己实验生成想要的复合多面体曲面。