解决方案
化学研究中可能经常需要绘制电子轨道,来描述原子或分子中电子的波函数。通常,它们是通过电子结构软件(如高斯程序 Gaussian)以多维数据集文件(Cube 文件)形式输出的。这些文件包含三维网格中给定轨道的体数据。
实现多维数据集文件可视化的应用程序有很多(如 VMD 或 GaussView),但我在这里想利用 Mathematica 的功能来轻松地合并图形, 以及使用它的过程自动化能力来高效地创建动画中的帧。
首先,我们需要一个从多维数据集文件中提取数据的函数。在这个过程中, 我们将创建一个 XYZ 文件的文本,这个格式也是由高斯开发的。函数 OutForm 用于模拟其他编程语言中的 printf 函数。
OutForm[num_?NumericQ, width_Integer, ndig_Integer,
OptionsPattern[]] :=
Module[{mant, exp, val},{mant, exp} = MantissaExponent[num];
mant = ToString[NumberForm[mant, {ndig, ndig}]];
exp = If[Sign[exp] == -1, "-", "+"] <> IntegerString[exp, 10, 2];
val = mant <> "E" <> exp;
StringJoin@PadLeft[Characters[val], width, " "]
];ReadCube[cubeFileName_?StringQ] := Module[
{moltxt, nAtoms, lowerCorner, nx, ny, nz, xstep, ystep, zstep,
atoms, desc1, desc2, xyzText, cubeDat, xgrid, ygrid, zgrid,
dummy1, dummy2, atomicNumber, atomx, atomy, atomz, tmpString,
headerTxt,bohr2angstrom},
bohr2angstrom = 0.529177249;
moltxt = OpenRead[cubeFileName];
desc1 = Read[moltxt, String];
desc2 = Read[moltxt, String];
lowerCorner = {0, 0, 0};
{nAtoms, lowerCorner[[1]], lowerCorner[[2]], lowerCorner[[3]]} =
Read[moltxt, String] // ImportString[#, "Table"][[1]] &;
xyzText = ToString[nAtoms] <> "\n";
xyzText = xyzText <> desc1 <> desc2 <> "\n";
{nx, xstep, dummy1, dummy2} =
Read[moltxt, String] // ImportString[#, "Table"][[1]] &;
{ny, dummy1, ystep, dummy2} =
Read[moltxt, String] // ImportString[#, "Table"][[1]] &;
{nz, dummy1, dummy2, zstep} =
Read[moltxt, String] // ImportString[#, "Table"][[1]] &;
Do[
{atomicNumber, dummy1, atomx, atomy, atomz} =
Read[moltxt, String] // ImportString[#, "Table"][[1]] &;
xyzText = If[Sign[lowerCorner[[1]]] == 1,
xyzText <> ElementData[atomicNumber, "Abbreviation"] <>
OutForm[atomx, 17, 7] <> OutForm[atomy, 17, 7] <>
OutForm[atomz, 17, 7] <> "\n",
xyzText <> ElementData[atomicNumber, "Abbreviation"] <>
OutForm[bohr2angstrom atomx, 17, 7] <>
OutForm[bohr2angstrom atomy, 17, 7] <>
OutForm[bohr2angstrom atomz, 17, 7] <> "\n"];
, {nAtoms}];
cubeDat =
Partition[Partition[ReadList[moltxt, Number, nx ny nz], nz], ny];
Close[moltxt];
moltxt = OpenRead[cubeFileName];
headerTxt = Read[moltxt, Table[String, {2 + 4 + nAtoms}]];
Close[moltxt];
headerTxt = StringJoin@Riffle[headerTxt, "\n"];
xgrid =
Range[lowerCorner[[1]], lowerCorner[[1]] + xstep (nx - 1), xstep];
ygrid =
Range[lowerCorner[[2]], lowerCorner[[2]] + ystep (ny - 1), ystep];
zgrid =
Range[lowerCorner[[3]], lowerCorner[[3]] + zstep (nz - 1), zstep];
{cubeDat, xgrid, ygrid, zgrid, xyzText, headerTxt}
如果需要创建多维数据集文件,可以使用以下函数:
WriteCube[cubeFileName_?StringQ, headerTxt_?StringQ, cubeData_] :=
Module[{stream},
stream = OpenWrite[cubeFileName, FormatType -> FortranForm];
WriteString[stream, headerTxt, "\n"];
Map[WriteString[stream, ##, "\n"] & @@
Riffle[ScientificForm[#, {3, 4},
NumberFormat -> (Row[{#1, "E", If[#3 == "", "+00", #3],
"\t"}] &), NumberPadding -> {"", "0"},
NumberSigns -> {"-", " "}] & /@ #, "\n", {7, -1, 7}] &,
cubeData, {2}];
Close[stream];]
接下来,我们需要用该函数来绘制轨道:
CubePlot[{cub_, xg_, yg_, zg_, xyz_}, plotopts : OptionsPattern[]] :=
Module[{xyzplot, bohr2picometer, datarange3D, pr},
bohr2picometer = 52.9177249;
datarange3D =
bohr2picometer {{xg[[1]], xg[[-1]]}, {yg[[1]],
yg[[-1]]}, {zg[[1]], zg[[-1]]}};
xyzplot = ImportString[xyz, "XYZ"];
Show[xyzplot,
ListContourPlot3D[Transpose[cub, {3, 2, 1}],
Evaluate[FilterRules[{plotopts}, Options[ListContourPlot3D]]],
Contours -> {-.02, .02}, ContourStyle -> {Blue, Red},
DataRange -> datarange3D, MeshStyle -> Gray,
Lighting -> {{"Ambient", White}}],
Evaluate[
FilterRules[{plotopts}, {ViewPoint, ViewVertical, ImageSize}]]]
];
让我们来看一个实例。首先,复制并在浏览器中打开此链接:https://dl.dropboxusercontent.com/s/rdsxcnqudn1s76n/cys-MO35.cube ,这是一个多维数据集文件,将该文件保存到你的基目录下:
{cubedata,xg,yg,zg,xyz,header}= ReadCube["cys-MO35.cube"];
然后通过下式绘图:
CubePlot[{cubedata, xg, yg, zg, xyz}]
如果要制作一个动画文件,我们当然希望所有的图像都具有完全相同的视角(ViewAngle)、视点(ViewPoint)和视图中心(ViewCenter)。当将这些选项赋给 CubePlot 时, 它将直接提供给 Show 函数。
vp = {ViewCenter -> {0.5, 0.5, 0.5},
ViewPoint -> {1.072, 0.665, -3.13},
ViewVertical -> {0.443, 0.2477, 1.527}};CubePlot[{cubedata, xg, yg, zg, xyz}, vp]
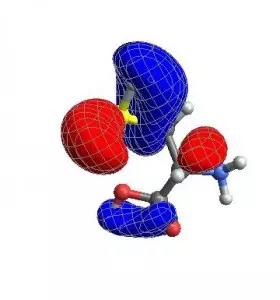
最后,您还可以使用通常用于 ListContourPlot3D 的任何选项。
CubePlot[{cubedata, xg, yg, zg, xyz}, vp,
ContourStyle -> {Texture[ExampleData[{"ColorTexture", "Vavona"}]],
Texture[ExampleData[{"ColorTexture", "Amboyna"}]]},
Contours -> {-.015, .015}]

ASAP/APEX技术交流群 373021576
SYNOPSYS光学设计与优化交流群 965722997
RP激光软件交流群 302099202
武汉墨光科技有限公司
友情链接
Copyright © 2012-2021 武汉墨光科技有限公司版权所有
许可证:鄂ICP备17024342号-1

