解决方案
穷举法可以解决很多问题,当数据规模变大时,需要一些优化技巧,剪枝就是一个常用手段,穷举+剪枝就是回溯算法了。
数独游戏,一行代码搞定N皇后问题,0.1秒玩胜Matlab之父Cleve Moler的四阶幻方!
在Wolfram Mathematica中处理这类问题很简洁,常用写法是排列组合函数(Tuples、Permutations、Subsets等)配合Select,或者使用列表操作进行迭代,经常两三行就能解决问题。不过也有缺点,这些排列组合函数是一次性生成一个大列表不是惰性求值,数据规模一大甚至会耗尽内存,速度也不一定快。
如果要换一种写法,自然就会想到使用(多重)循环或递归了,Mathematica中循环的效率不算高,但是可以配合编译(Compile)来大幅加速。比起递归,多重循环其实更容易被编译器优化,多数编程语言中,层数很多的循环再层层嵌套If,写起来麻烦,看起来实在感人,可扩展性也差,通常要避免。不过Mathematica具备像LISP中“数据即代码,代码即数据,一切都是表达式”和擅长符号计算等特性,我们可以很方便的进行元编程(Meta-Programming),通过写代码来动态生成代码再编译,从而对程序加速,有时可以接近C语言的速度。
数独游戏

数独是一种数学逻辑游戏,游戏由9×9个格子组成,玩家需要根据格子提供的数字推理出其他格子的数字,需要满足每一行、每一列、每一个粗线宫 (3x3) 内的数字均含1 - 9,不重复。这种游戏只需要逻辑思维能力,与数字运算无关。虽然玩法简单,但提供的数字却千变万化,所以不少教育者认为数独是锻炼脑筋的好方法。
求解数独的方法有很多种,目前网上相关的Mathematica程序,能求全解的速度慢,速度快的基本都是只能得到一个解。而下面这种方法简单粗暴,既可以得到所有的解,速度也还行,要改成只返回一个解的也不难,而且可以进一步编译为C代码加速。
输入数独矩阵,将其中的0(空白处)都替换为符号变量
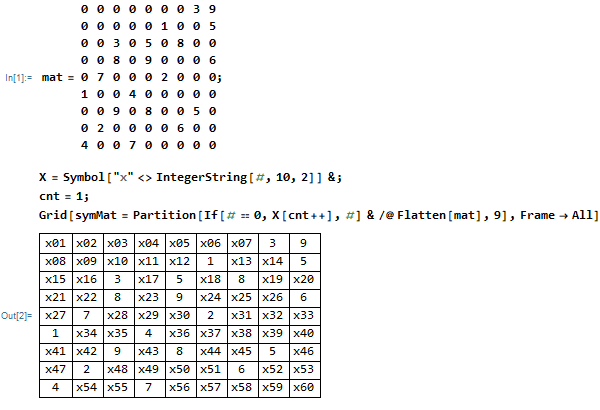
根据数独的规则,得到约束条件

根据约束条件构造迭代器范围(iterator specification)
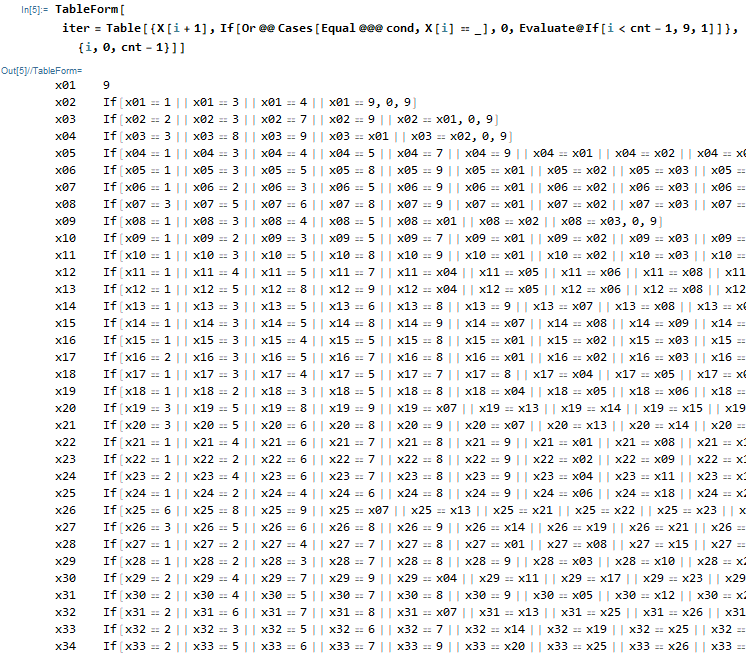
创建编译函数并开始计算,这其实相当于一个60层的循环
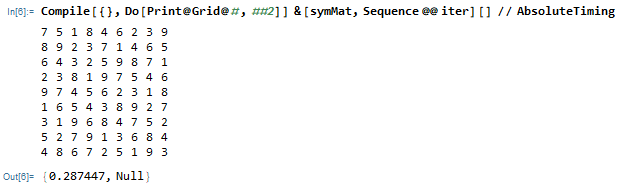
根据上面的思路,很容易封装一个函数sudokuSolve,求解Project Euler第96题的所有50个数独,耗时约1.5s,求解一个多解数独的全解(有一百多万个解),耗时约15秒。测试电脑CPU为移动端9代i7。
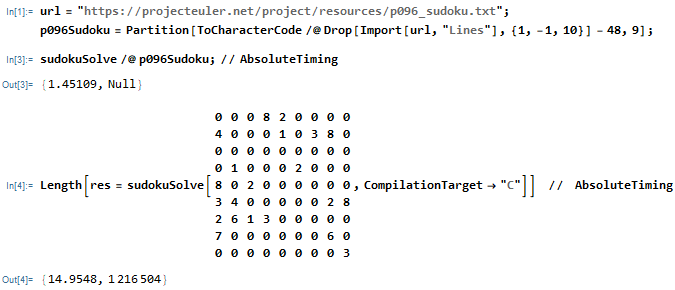
上面的代码还能继续优化,比如有些数独经过转置或反转后算得会更快,有兴趣的读者可以尝试从这个角度改进。
N皇后问题
八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法?八皇后问题可以推广为更一般的n皇后摆放问题:这时棋盘的大小变为n×n,而皇后个数也变成n。
追求简洁的话,一行代码就能搞定 Select[Permutations[v = Range@8], And @@ Unequal @@@ {# + v, # - v} &] 然而,随着皇后数量的增多,当n=12时,一般电脑的内存都不够用了
使用迭代的版本,当n=12时,耗时5秒,比之前有进步,但还是不够快

使用多重循环剪枝的版本,当n=15时,只需3.6秒,考虑到对称性减少一些计算耗时2.4秒。简单起见,这里只进行计数,没有收集具体的解,如果要收集所有的解使用Internal`Bag也只需4秒多一点。

作为比较,维基百科上(https://zh.wikipedia.org/zh-hans/八皇后问题)的两个C语言示例程序,当n=15时,耗时也都在3.7秒以上,使用位运算优化过的版本(https://blog.csdn.net/hackbuteer1/article/details/6657109)耗时1.1秒,C代码都使用的GCC编译器开了O3优化。
四阶幻方

把1~16的数字填入4x4的方格中,使得行、列以及两个对角线的和都相等, 满足这样的特征时称为:四阶幻方。 幻方的一般性质为:幻方每一行之和、每一列之和、两条对角线之和都相等,都等于幻和(四阶幻和为34)。
求解所有四阶幻方,用全排列搜索空间太大,对16个数全排列有16!=2.09228*10^13种不同情况。根据幻方的性质,可以先求解下面的不定方程,然后再遍历7个变量,这样就减少到 A(16,7) = 16! / 9! = 57657600 种组合,极大缩小了搜索量。

Matlab中有个magic函数,可以方便的生成幻方,但是只能生成单个,要生成所有的四阶幻方,Matlab之父Cleve Moler曾经写过一篇相关的博文并分享有代码 https://blogs.mathworks.com/cleve/2012/11/26/magic-squares-meet-supercomputing/ ,还有一篇相关的论文(https://pdfs.semanticscholar.org/dcdb/c3d9e7e31b14d9f9c1a94d4678258f077917.pdf)也是使用Matlab实现的。
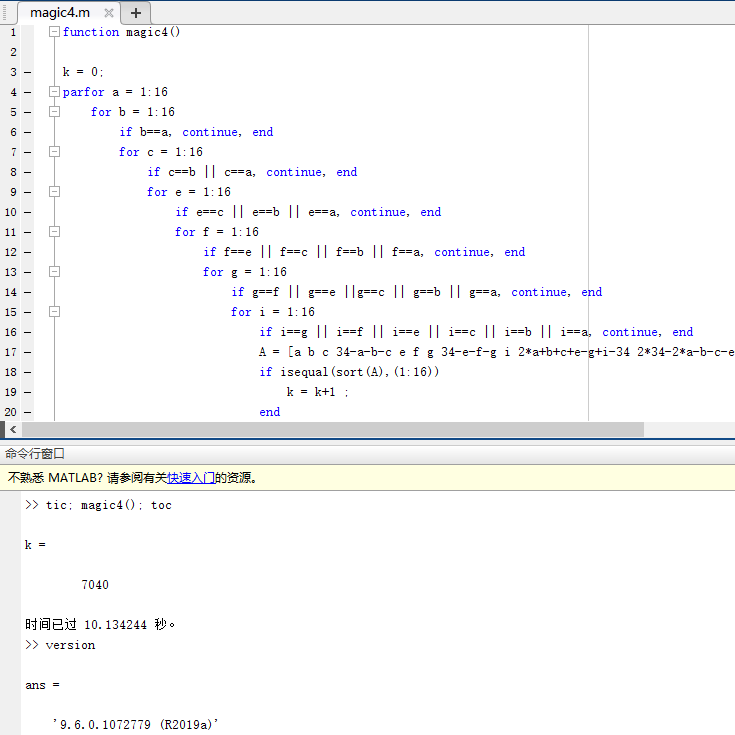
为了简单起见对代码稍作修改,只统计个数,在Matlab R2019a中,使用并行计算耗时约10秒(第一次启动并行工具箱需要等待,计时时已经启动过了)。相应的Mathematica代码为4.4秒。

进行更好的剪枝之后,耗时不到0.1秒。

ASAP/APEX技术交流群 373021576
SYNOPSYS光学设计与优化交流群 965722997
RP激光软件交流群 302099202
武汉墨光科技有限公司
Copyright © 2012-2021 武汉墨光科技有限公司版权所有
许可证:鄂ICP备17024342号-1

