12.1 是迄今为止最大的.1版本发布：182个新函数，还包括成百上千个现有函数的更新和改进；支持高清像素HiDPI；视频也可以计算，语音转换成文字易如反掌；完全掌控各种数据结构，渐近超级函数，无所不能的DSolve，工业级别的凸优化，清晰明了的矢量绘图，优雅的断面线，层次清晰的素描画，灵活操作Dataset，GANs、BERT、GPT-2、ONNX 等最新的机器学习技术；自动证明苏格拉底不会永生；为万物定位，海量的资源库告诉你食物的烹饪时间等；分子识别，分子轨道的导入；与Julia、Ruby 和 R 的连接；程序包和万能的注解等等等！

我们很高兴地看到，虽然现在新冠病毒疫情影响到很多员工和公司的正常经营，但我们还是能够如期发布产品。（感谢我们辛勤付出的团队，我们的一部分员工远程工作的时间已经有十年以上了。）

迄今为止最大的.1发布

这常常是个有趣的时刻：我们要打包一个.1版本——来发布我们的研发成果。我想，“这会是一次大型发布吗？”当然，我知道我们自从去年四月发布12.0版本以来做了大量的工作，包括所有这些设计和我们研发出的新内容。

但是在我们开始制作新版本的更新内容列表时发现，天呐，简直写不完。不同的团队可能在很早以前就开始开发哪个小项目，或者在项目中添加了新函数，或者哪里又有一些创新，等等等。

我们从三分之一个世纪前开始开发1.0版本的时候，旅程就开始了。在这些年之后，可以看到每一个新版本的发布都让这个产品变得更加强大。

所以我们在制作12.1版本的新内容列表时，我们想，“这会是我们迄今为止最大的.1版本发布吗？”。然后现在我们终于得到了答案：“是的，绝对是的”。

函数的数量虽不是最好的衡量方法，但是也说明了一些事情。在12.1版本中，有182个新函数，还包括成百上千个现有函数的更新和改进。

现在来看看：HiDPI

在1988年的时候我们发布了1.0版本，那时普通的电脑分辨率只有640像素（那时候还是CRT显示器）。最近我在用一些我1990年代时候使用过的笔记本（是的，它们现在还能用，这真的很棒！），发现它们那时只能在一个那么小的窗口打开。但是今天当我在打这些字的时候，我的面前是两个3000像素的屏幕，而且4k屏幕也很普遍了。所以我们为12.1做的其中一件事，是加上了全系统对高清像素显示的支持。

有人觉得这个可能很简单，认为这个是“和操作系统在一起的”。但是其实为了支持HiDPI，我们整整花了两年的时间才实现这一功能。在仔细设计了1000个图标和其他从位图到可以适应任何尺寸的算法图形，所有关于光栅化的内容（不止为了光栅化，还为了三维图形纹理等）都需要重新做。所有内容的尺寸——包括它们与操作系统这些年来引入的一些不成熟产品的交互界面——都必须重新界定和思考。

但是现在这个任务已经完成了。我们可以用于任何分辨率的屏幕：

顺带提一句，说到显示，另一个12.1版本的“基础架构“改进是在macOS和Windows上，用Metal和Direct3D 11渲染三维图形。它们不仅让3D图形变快了一点，还为多线程渲染、VR、AR等等任务奠定了基础。

视频计算的开始

我们朝这个目标努力了15年，现在终于做到了：使用视频进行计算。我们在2008年把图像引入了语言；2016年把音频引入了语言。在12.1中，我们首次推出视频计算。在未来的发布中肯定还会有更多功能，但是这在12.1中已经有很多功能了。

所以就像Image和Audio可以用符号表示图像和音频一样，我们现在有了Video。

下面从一段视频中提出了五帧：

这段为每帧的平均颜色做了一个时间序列：

然后就可以绘制这个时间序列了：

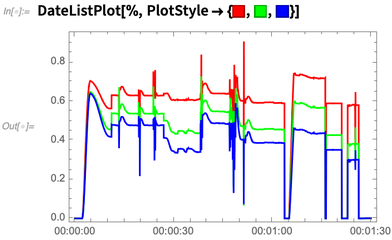
视频是一个很复杂的领域，为了不同的最优化目的会有很多不同的编码。在12.1版中，我们可以支持其中的250多种编码，进行导入、导出和转码。你还可以指定网络上的视频：

而且重要的是，现在视频已经可以整合进所有内容。比如你可以立刻对视频使用图像处理或音频处理或机器学习函数。下面是一个在上述视频中绘制汽车地点的范例：

假设你有一个Manipulate函数，或者一个动画（假定是来自ListAnimate的）。现在你可以立刻用它做一段视频：

你可以加上音频，然后把整个文件导出到文件夹、云端等等。

所以这个新的视频功能是否具有工业意义呢？我为一个我手边正在做的新项目已经录制了上百个小时的视频了。所以我决定用这些资源来试验一下新功能。效果非常好！我可以录制4个小时的视频，然后从视频中立刻抓取一批样本帧——是的，就在几个小时的CPU时间内——“概述了整个视频”，方法是使用SpeechRecognize把所有语音转换为文字然后生成一个文字云：

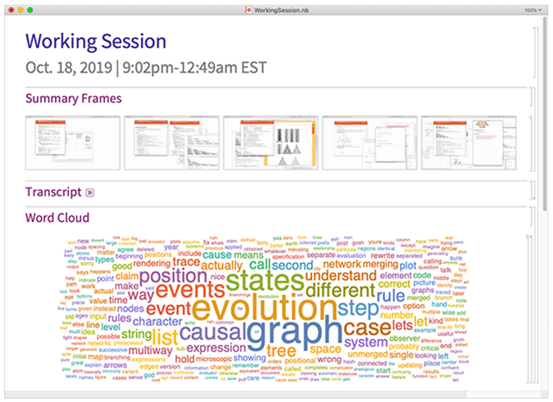
说到音频，在12.1版本里还有个新内容。我们为笔记本内置音频对象重新做了GUI，然后引入了SpeechInterpreter，有点类似于Interpreter函数的说话版本，这里我们使用一段音频对象然后返回了在音频中提到的航空公司名称：

在12.0版本中我们引入了一个重要函数TextCases，可以从上百种“文本内容类型”中提取文本（这个函数在现在的12.1版本中有自己的文档页面了）。12.1中我们还引进了SpeechCases，对音频内容可以执行同样的任务。

一个计算机科学的故事：DataStructure

我们的一个长期项目是为Wolfram语言开发一个以本地机器代码为目标的全功能编译器。12.0版本率先发布了这个开发成果，12.1版本中的内容是这个项目的一个副产品——其实也是一个非常重要的项目内容：新的DataStructure函数。

我们过去策划过很多领域的内容：化学、方程、电影、食品、导入导出格式、单位、API等等。在每个内容里我们都让这些内容可以直接无缝地被Wolfram语言计算。现在我们要加入另一个类别了：数据结构。

回想一下所有那些在课本、论文、图书馆等地方提到的数据结构。我们的目标是让它们可以无缝被Wolfram语言使用，并可以直接在汇编代码中访问。当然这个工程量很大，而且我们已经有一个共用的“数据结构”：Wolfram语言的符号表达式。在Wolfram语言的内部，我们一直在使用各种数据结构，为不同目的最优化，并由我们的算法和元算法自动挑选。

但是现在有DataStructure，就出现了新的内容。如果你有一个希望使用的特殊的数据结构，只需要用名称调用它，然后就可以使用了。

下面展示了你如何构建一个有链接的列表数据结构：

在链接列表中追加一百万个随机整数（在我的机器上只用了380毫秒就完成了）：

现在就可以立刻生成结构的可视化效果：

下面可以计算所有值的数值平均：

DataStructure可以用来进行小规模的比如以教育为目的的任务，也可以进行大型工业化强度的任务。如果你在教授一门关于数据结构的课程，你可以直接使用Wolfram语言，把所有东西存储在你的笔记本中，自动可视化你的数据结构等。如果想建立大型生产类代码，你可以最优化你现在正在使用的数据结构并对之有完全的掌控。

DataStructure是怎么工作的呢？首先它是由Wolfram语言写成的，并使用编译器进行编译（编译器也是用Wolfram语言写成的）。

在版本12.1中，我们涵盖了大多数基本数据结构，其中包括各种列表、数组、集合、堆栈、队列、哈希表、树等。其中重要的一点是：每个文件都记录了其各种操作的运行时间（“O(n)”, “O(n log(n))” 等），并且代码确保了此操作是正确的。

要看写DataStructure的经典算法也很简单。

创建一个二叉树数据结构（并将其可视化）：

下面的函数用于平衡二叉树：

现在进行运算，并可视化结果：

渐近超级函数

你现在有一个符号表示的数学表达式，然后你想要弄清楚它的大概值。如果这是一个数字那你只需要使用N获取一个数字近似值。但是你如何获取一个符号近似值？

从1.0版本开始——且从整个数学历史1600年代开始——就有了幂级数的概念：找一个近似函数的类多项式，就想Series一样。但是不是每个数学表达式都可以很好地像这样找到近似。这个数学内容很难，但是如果可以实现的话会非常有用。我们在版本11.3中为一些特定情况（比如积分）引入“渐近逼近”函数，在12.1版本中，我们引入了渐近超级函数Asymptotic。

思考下面这个拉普拉斯逆变换：

没有一个精确的符号解。但是当 t 趋近于0时有一个近似渐近：

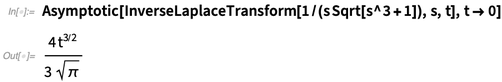
有时为了方便，甚至可以不用进行精确计算，就原样留着给Asymptotic进行计算：

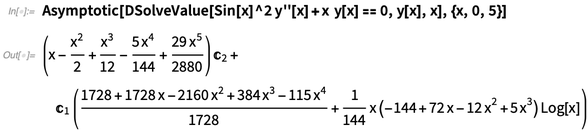
Asymptotic可以处理连续变量的函数。在12.1版本中，还有一个DiscreteAsymptotic。这里我们想知道Prime函数的近似行为：

或者阶乘：

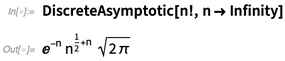
我们还可以根据需要使用更多项：

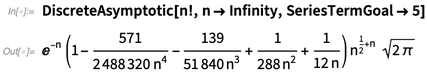
有时甚至一些简单的函数可以生成很奇异的渐近逼近：

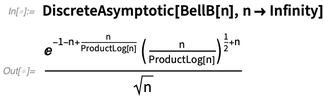
像往常一样，更多数学内容

数学的空间很广阔也很重要。对于Wolfram语言（也对于Mathematica来说），我们总是不断尝试用数学进行更多计算。

长期以来我们都在致力于特殊函数。在版本1.0时我们已经有70个特殊函数了。这些函数涵盖了单变量的超几何函数，在3.0中加入了通用 pFq 的情况。在这些年中，我们逐渐增加了一些其他超几何函数（和250个其他类的新的特殊函数）。一般的超几何函数是有三个正则奇点的微分方程的解。但是在12.1版本中我们已经将其广义化了。现在我们有Heun函数，可以解有四个正则奇点的方程式。这听起来好像没什么，但是实际上这是一个数学的危险地带——就比如192个已知的特定情况。它们现在受到很多人关注，因为它们出现在黑洞、量子力学、共形场论的数学中。Heun函数有很多参数：

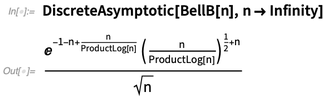
顺便说一句，当我们“支持一个特殊函数”时，可以用它做很多事情。不仅仅是可以在复平面中以任意精度计算函数的问题（虽然这个已经足够复杂了）。我们还需要可以计算渐近逼近、简化、奇点等。而且我们要保证这个函数可以生成在类似Integrate、DSolve、Sum的函数结果中。

我们一直以来有一个目标就是把像DSolve这样的超级函数变得“无所不能”。为了确保我们的算法可以处理任意问题，可以处理我们在任何地方读到的尽可能多的情况。实际上，这些年来，我们在这方面已经做的很好了。但是在12.1中，我们有了进一步的重大发展，尤其是DSolve的开发。

下面是一个例子（是的，刚好需要用到Heun函数）：

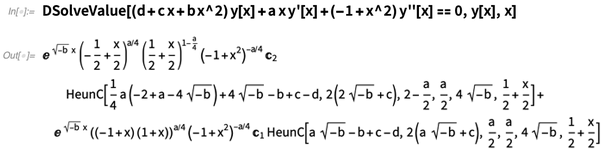
在1940年代有一本很著名的数，叫做Kamke，是一本拥有海量微分方程解答的集合，其中包括一些非常罕见的情况。我们快要可以完成这本书中100%的（具体）方程了（还在测试最后一点）。

在12.0版本中，我们为绘制复变量的复函数引入了类似ComplexPlot和ComplexPlot3D这样的函数。在12.1中，我们现在支持绘制复等高线图。这里我们有一个根据复函数的AbsArg得到的两组等高线：

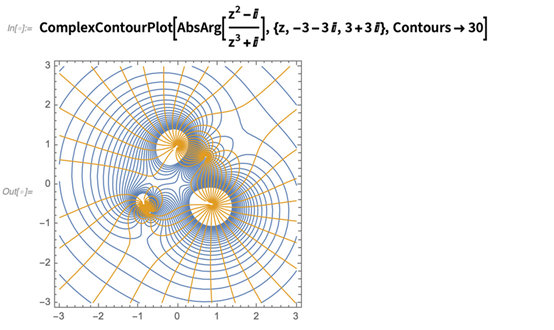
12.1版本还更新了ComplexRegionPlot，可以有效解决复平面中的方程式和不等式。比如这里方程的（分枝切割）解，其模拟解在实数区间为平凡解：

在与之不同的另一个数学领域中，版本12.1还有一个新函数CategoricalDistribution。我们在第6版中引入了统计分布的符号表达，使用NormalDistribution和PoissonDistribution这样的函数，而且这个推出是很成功的。但是到目前为止，我们支持的分布只是针对数字的。在12.1版本中，我们第一次支持输出结果不是数字的分布。

下面这个范例中，指定概率的分布结果是x，y，z：

有了这个分布，我们可以生成随机变量：

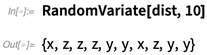
下例是一个三维的类别分布：

我们现在可以求这个分布的概率分布函数，想要求获取A，D，Y情况的概率是：

顺便说一句，如果你想“查看分布”，你可以点击概述部分的+键，或者使用Information：

CategoricalDistribution有很多种用法，比如在机器学习中，下例我们来创建一个分类器：

如果我们只是输入2.3，这个分类器会给出其能给出的最好的猜测结果：

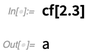
但是在12.1中，我们还可以让它生成一个分布，结果是一个CategoricalDistribution：

最优化的前沿技术

在12.0中我们引入了工业级别的凸优化。我们可以用这个功能解决大部分常见的问题种类（比如线性、半正定、二次曲线和圆锥曲线）。但是有一个还没有照顾到：几何优化。现在我们在12.1中加入这个功能：

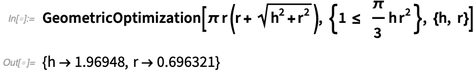
你可以用GeometricOptimization解决各种实际问题，如果需要的话可以使用上千个变量。比如，考虑设计在x和y上偏序的某个尺寸的矩形。为了让这个问题更具体，你可以给出一批不等式：

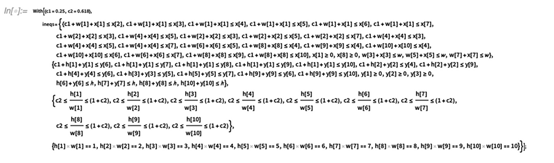
只需要一秒钟就可以生成最优解：

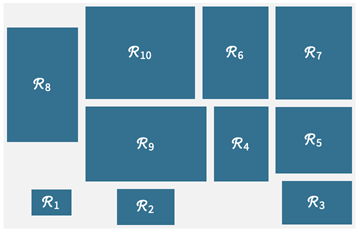
在最优化中，通常有两个大类：连续和离散。我们12.0中凸优化方程解决了连续变量的情况。但是在12.1中，最主要的新内容是增加了离散（比如整数）变量和离散连续混合变量的支持。

下面是一个很简单的例子：

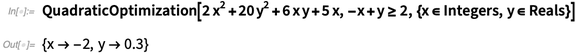
如果 x 没有被限定是一个整数，那么结果会不一样：

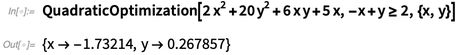
但是，对于我们其他的最优化功能——当然这可以再升级，尽管其中运用到的组合最优化在计算上肯定更为复杂（比如经常是NP完备的）。而且实际上我们可以做这类大规模运算的唯一原因是我们已经实现了一个新的以迭代为基础的技术，可以成功地解锁混合凸优化。

解决向量绘制问题

在这40年中我一直在尝试矢量绘制问题，但是在过去一直没有成功。如果矢量太短，你看不到它们的方向，如果你做的太长他们又会互相撞到一起。但是在我们12.0成功解决ComplexPlot问题后——这已经拖得太久了——我们决定在12.1中一次性全部解决矢量绘制的问题。现在我很高兴地宣布，我们做到了。

所以现在，你可以用VectorPlot（包括所有相关函数）来做矢量绘制，而且你会自动得到一个可以很好表现你的矢量的图：

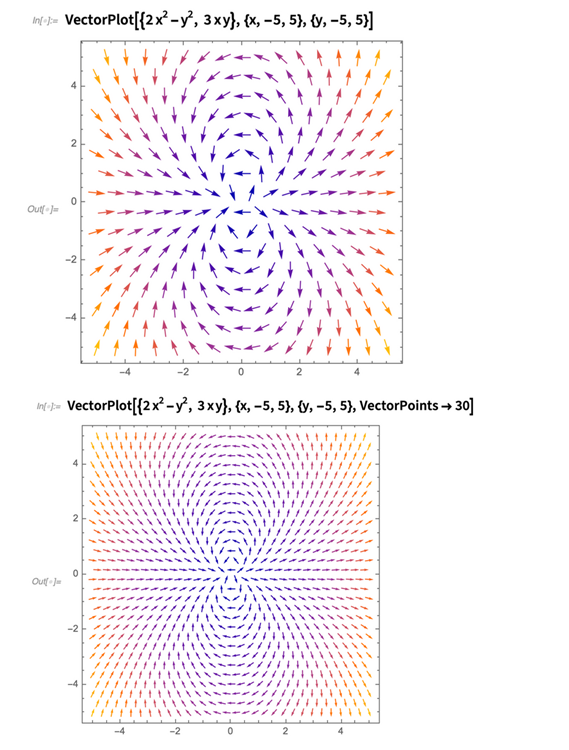
难点在哪里呢？这基本是关于把矢量放在一个六边形网格中，而且视觉上更统一了。（你也可以做其他你想要的选择。）然后就是选择适合的比例颜色来代表矢量大小了。

当然还有别的挑战，比如在一个区域内绘制矢量：

把向量绘制结合我们的复数绘制功能，我们在12.1中还有ComplexVectorPlot：

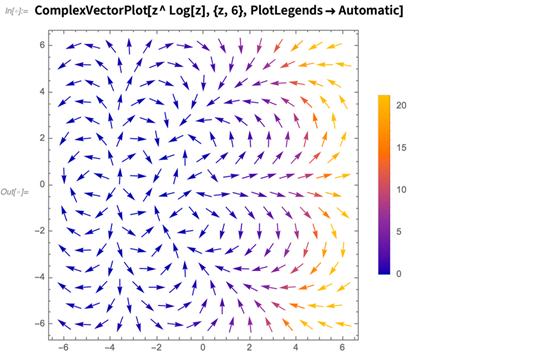
断面线

在此之前是灰度的概念，然后才有断面线。如果你看100年前的书籍，你会看到各种用断面线绘制的优雅的图案，现在我们也可以做到这个了。

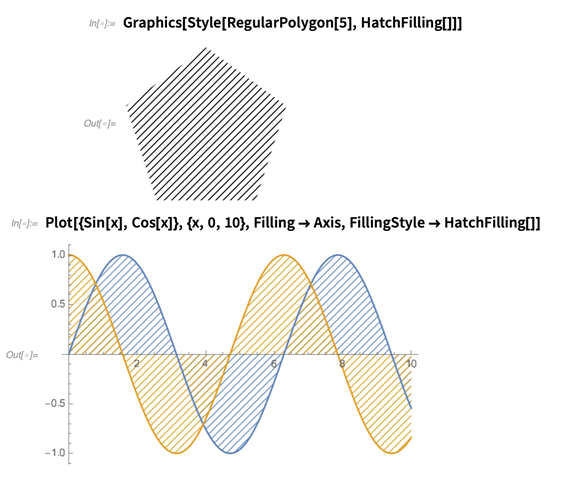
当然，所有内容都是可以计算的：

我们还有一个重要的断面线的函数：PatternFilling。下面是一些已命名的模式的范例：

你也可以用任意图像当做模式：

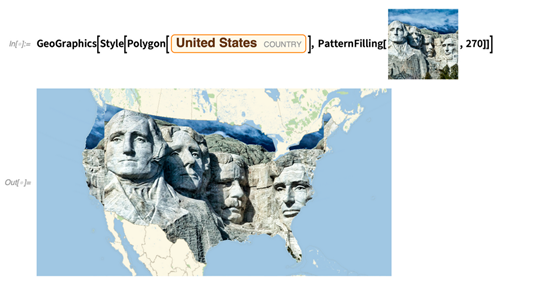
12.1版本中还有这些种类纹理的三维泛化：

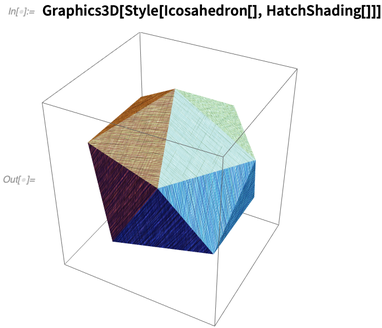
甚至黑白效果下看着也很不错：

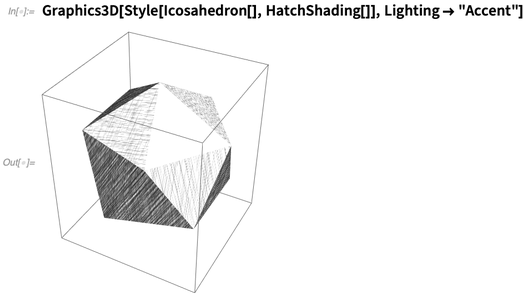
下面是点画阴影的范例：

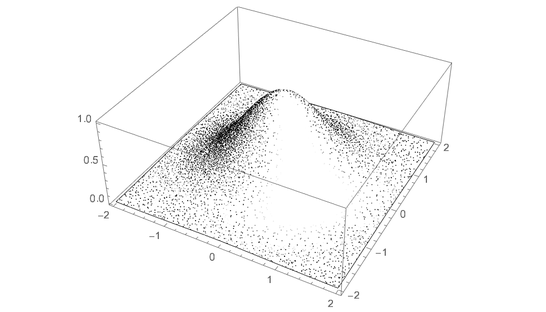
计算拓扑学的开始

在过去的几个版本中，我们深入引入了计算几何学。在未来的版本中，我们还要支持更多关于计算拓扑学的内容。12.0中我们已经有EulerCharacteristic和PolyhedronGenus，12.1中我们引入几个强大的函数来处理单纯复合型的拓扑学内容，比如可以用于表示网格上。

这就为十二面体的的0维分量，比如角，提供了一个连通图：

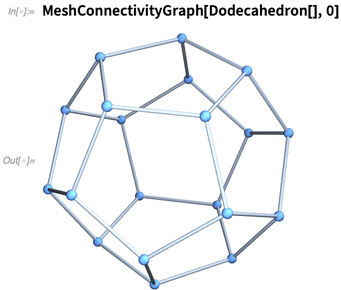
下面是十二面体中线到线的连通图：

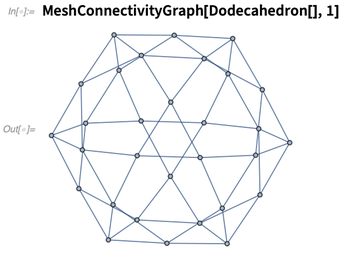
下面是角到面的连通图：

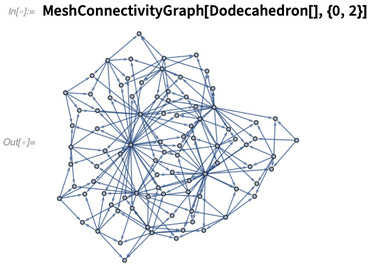
这是一个非常泛用的函数，下面是门格海绵中不同维数单元格的图形：

给定一个网格，做拓扑搜索通常很有用。比如，下面是一个冯洛诺伊网格：

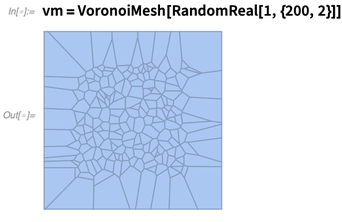
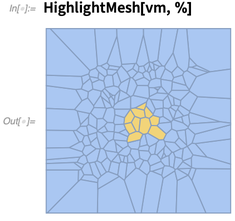
下面是10个离位置{.5, .5}最近的网格单元格（每个前面的2代表了这些都是二维单元格）：

现在高亮这些单元格：

表格数据：计算和编辑

从第一次出现在10.0中以来，Dataset取得了巨大的成就。在12.1中我们开始升级和扩展Dataset的功能。

第一件事是一件刚刚发生你可能没有注意到的事情。当你在笔记本中看见Dataset，你只是看见了它的展示形式。但是通常如果你向下滑动展开的时候可能会有一些额外的数据。在12.1中，Dataset自动在笔记本中储存这些额外数据（至少是$SummaryBoxDataSizeLimit里面确定的数据大小），这样如果你再次打开笔记本，Dataset都在那里随时准备好了计算。

在12.1中，我们做了很多关于与Dataset的格式相关的内容。比较基础的是可以设置默认要展示多少行多少列：

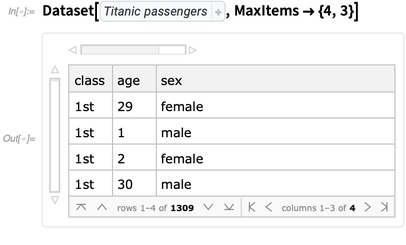
在版本12.1中，有很多允许很细节的对如何展示Dataset的编程控制选项。下面就是一个简单的范例：

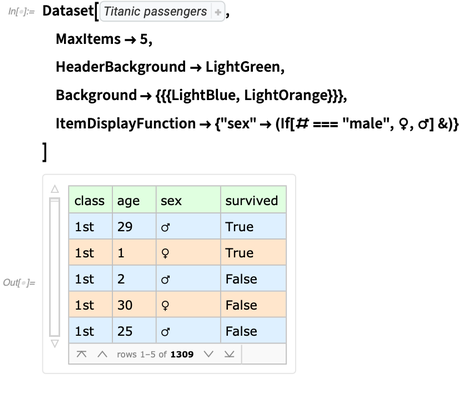
一个比较重要的新功能是“右击”的交互（可作用于行、列和单个项目）：

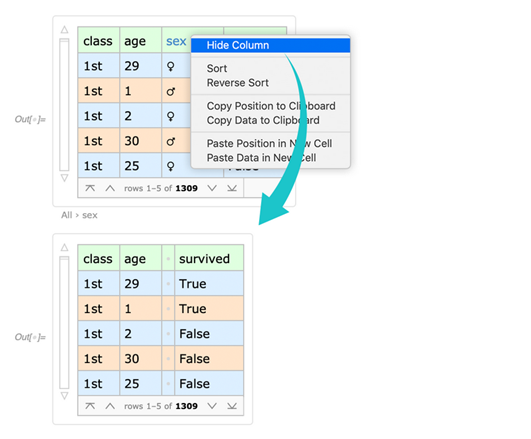
Dataset是一个可以展示并计算任何深度表格数据的强大工具。但是有时候如果你只想输入或者编辑简单的二维表格数据，那么用户对界面的要求就会与Dataset提供的有很大差异。所以在12.1中，我们还实验性地引入了一个新函数TableView，这就是让用户输入并查看的一个界面，是个简单的二维表格数据：

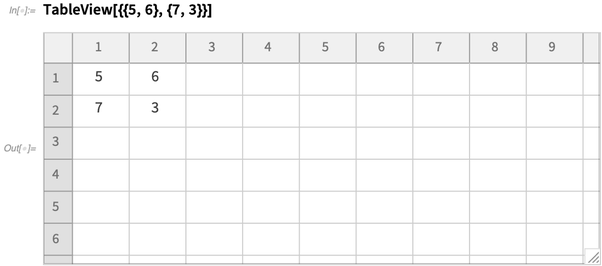
就像一般的工具表一样，TableView有固定宽度的列，你可以人工调整这个宽度。它可以有效处理大规模数据（比如上百万个项）。项可以是（默认）数字或字符串。

当你完成编辑TableView，你可以使用Normal，然后就可以获取一个数据列表（也可以直接传进Dataset）。TableView可以像一般的工作表一样让你把数据放在你想要的地方，如果数据中有一个“空洞”的话，那么在你生成的列表中会显示Null。

TableView其实是一个动态控制。所以，比如说用TableView[Dynamic[x]]你可以编辑一个TableView，然后让其负载自动成为某个变量 x 的值。（是的，所有这些都可以在对表示 x 的值的表达式进行最小更新的情况下有效完成。）

GANs、BERT、GPT-2、ONNX：
最新的机器学习技术

机器学习现在正流行。当然我们很早之前就开始开发这项技术。我们在2014年的旗舰版中就引入了Classify和Predict这两个高度自动的机器学习函数，然后在2015年的时候我们引入了我们第一个基于神经网络的函数——ImageIdentify。

然后自此之后这些年间，我们为机器学习建立了一个强大的系统，尤其是对神经网络。有一些重点值得突出。首先，我们强调了高度自动——在尽可能多的地方使用机器学习来自动化，这样非专业人士也可以使用这些前沿技术。第二件事是，我们还在建立神经网络，这也就意味着我们已经提前训练了分类器、预测器和特征提取器，你可以立即无缝使用。另外一件大事是，我们整个神经网络可以符号化表示，也就是说神经网络可以计算、用符号构建，这样也就可以程序化地操控以及可视化了。

在12.1中，我们继续着我们在机器学习领域的前沿开发。我们Wolfram神经网络资源库中有25种新的神经网络，包括BERT和GPT-2。而且按照这些网络的设置方法，用户可以立即使用这些网络。（而且在12.1中，还支持新的ONNX神经网络通用标准，使得导入最新发布的任意格式的神经网络都更加简单。）

这就是我们资源库中GPT-2的符号表示：

如果你想看里面的内容，只要点击”-“，持续点击并向下拉可以看到更多内容：

现在你可以立即使用GPT-2，比如可以一次一个词条逐步生成一段文本。

（额……我想知道这是怎么训练来的……）

顺便说一句，人们时常说起机器学习和神经网络像是站在传统编程语言代码的另一端。某种程度上说这是对的。一个神经网络从真实世界的范例、经验中学习，而传统编程语言只是给出具体而抽象的标准，告诉计算机该做什么。我们现在有Wolfram语言，站在一个绝佳的位置，可以用这个全范围计算型语言和语言中所有这些精细的计算能力，对整个真实世界进行表示和计算。

过去几年中很高兴能看到机器学习逐步被整合进Wolfram语言。我们对一些超级函数非常感兴趣——如 Predict、Classify、AnomalyDetection、LearnDistribution 和SynthesizeMissingValues，这些函数都可以做“符号指定”的操作，但是使用神经网络和现代机器学习技术来做的。

在12.1中，我们还会在这个方向上努力下去，对使用复杂的神经网络工作流程的超级函数我们会继续开发，比如GAN。12.1版本引进了符号NetGanOperator和新选项TrainingUpdateSchedule。现在看起来我们只需要改这两项来让一般的 NetTrain 函数可与GAN一起使用。

一般GAN的设置是很复杂的（这也是为什么我们一直在设计可以方便使用GAN的超级函数）。下面是一个12.1版中GAN的使用范例：

注解的计算

你是如何为你正在计算的内容添加原数据注解的？在12.1中，我们可以使用一个通用注解框架——然后并用它们进行计算。

我们首先说一下图的范例。你的注解可以分为立即“在图中可见“的（比如顶点颜色），和不能在图中看到的（比如边的权值）。

下面是我们构建的一个有注解的图的范例：

然后我们对顶点进行注解：

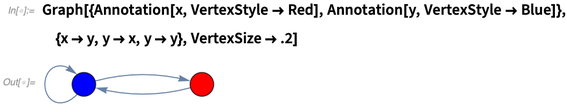
AnnotationValue让你可以询问注解的值：

AnnotationValue的一个重要功能是你可以对其赋值，比如设置g是这个图：

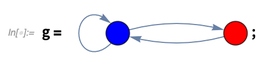
然后现在指定一个注解值：

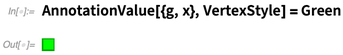
这样图就改变了：

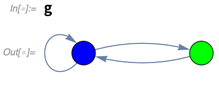
如果需要的话，可以随时删除注解：

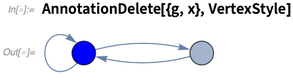
如果你不想要永久修改，只需要用Annotate生成一个有注解的新图（3和5是顶点的名称）：

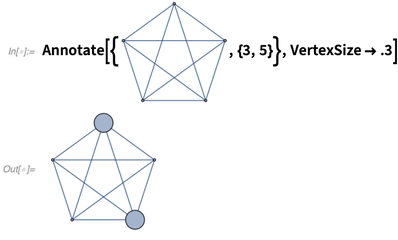
有一些注解对于在图上计算是很重要的。其中一个例子是边权重。下例将边权重的注解放入图中，但是默认不会把这个注解显示出来：

下例可以显示边权重：

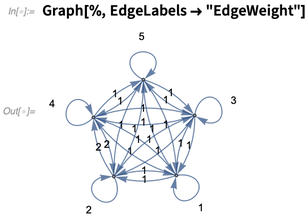
下例则使用该权重进行了计算：

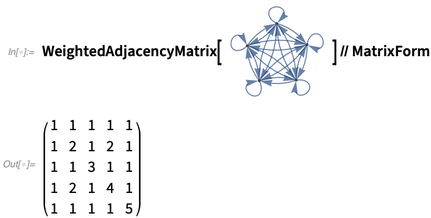
你可以使用自定义的注解：

下例检索了注解的值：

注解最终储存在AnnotationRules选项中：

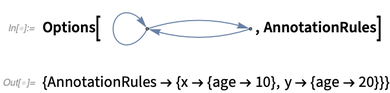
你可以把所有注解当做这个选项的一个设定。

注解主要复杂的地方在于判断在计算中它们什么时候该被保留、什么时候被合并、以及什么时候被丢弃。一般来说，只要注解有意义，我们就会保留它们：

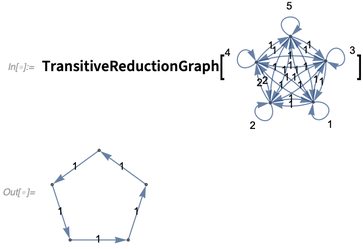
注解是一个非常常用的东西，不仅可以应用在图上，也可以用在其他构建中增长的数字上。在12.1中我们还为绘图应用添加了一点小功能，可以处理一些复杂的情况。当有多重图时，比如同个顶点有多条边。我们看下面这个图：

你怎么分辨这两条边？这不是一个注解的问题，而是你确实想分清楚这两条边，就像图中的顶点这么清楚一样。在12.1中，你可以为边命名（或叫做“标签“），就像你可以为顶点命名一样：

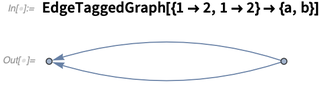
这样这张图上的边都用“标签“标明了：

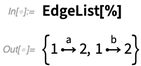
这些标签就是边说明标准的一部分：

我们回到注解这里来。另一个可以被标注解的对象是网格。这里我们为有样式的0维边界单元格做注解：

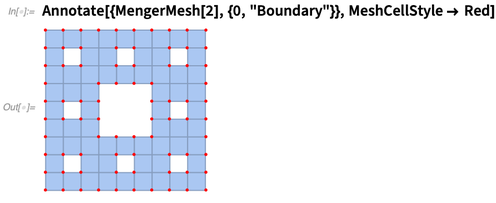
还有一个完全不同的可以做注解的结构是音频。下例为一个Audio对象注解了该段音频中哪里有语音端点：

这里检索了注解的值：

我们还在开发很多其他可以使用注解的地方。下一个就是图像。为了准备这个功能，在12.1中我们加了一些新功能到HighlightImage中。

现在HighlightImage可以使用注解信息了：

语言创新和扩展

Nothing是一个很成功的函数：

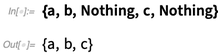
在Nothing之前，你总是需要戳开从外面拿来的列表然后才能把里面的元素删掉，但是Nothing可以“从内部工作”，是一个符号式的指定删除的方法。

就在我们开发出Nothing的时候，我们意识到，我们还需要另一个功能：一个可以大量将内容添加进列表的符号对象。之前大家都是用Sequence@@…来做这件事，但是Sequence并不好构建，这个惯用法也并不稳定。

我们现在的自动插入器定义起来非常简单。但是我们要怎么称呼它？这些年中这个非常有用的功能都亟待一个名称。有几次我们的直播设计回顾中都有人提到了这个问题。每次我们都要讨论好一会儿，当然会有好的名字提出来，但是每次都不是所有人都满意。

最后我们决定要解决这个问题。起名字的过程很痛苦，我们最长花过90分钟的直播时间仅仅用来讨论名称里是否要改变一个字母。但是最后，我们定下了Splice。Splice是拼接，就像胶片和DNA，这是一个插入内容的地方。所以在12.1中我们现在有下面的范例：

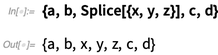
当然，更普遍的范例是像下面这样：

Splice还可以避免很多奇怪的（而且有可能也是有程序错误的）Flatten操作：

我们在开发Wolfram语言过程中一件经常尝试去做的事情是，分辨什么是可以包装进函数的重要的“计算块“（而且我们如何给这些函数一个好的名称！）。在12.1中，有一组新的处理列表中元素子集计算的函数：

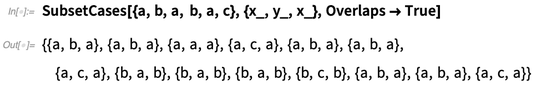
这些函数我肯定写过一亿次了。但是现在我们有一个人人都能用的函数。这些函数在很多地方出现过。而且实际上我们首先要执行与语义询问类型计算相关的通用版本。

但是理论上任何设计精细的函数最终都会被广泛使用，我最近就发现了SubsetReplace在基础物理背景下一个意想不到但是效果出奇好的使用方法。但是我们等下再详细说这个……

说到物理我想起了12.1中一点别的事情：处理时间的新函数。DateInterval现在提供时间区间的符号表示，而且需要定义一个挺有意思的代数排序，包括需要符号InfinitePast和InfiniteFuture：

函数式编程和其他

我们总是想让Wolfram语言变得更简单好用，而且12.1包括了我们在符号函数式编程开发过程中想要体现的理念。如果你把置入函数当成一个动词，我们现在就尝试加入一个副词：用于修饰这个动词。

第一个例子是OperatorApplied。下例是一个函数功能的基本范例：

为什么这个函数有用？很多函数有“运算符形式“。比如，可以不用这么写

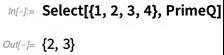
而是可以这么写：

这就意味着你可以使用这些修正的函数：

或者（使用Map的运算符）：

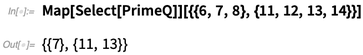
好了，那么OperatorApplied能干什么？基本上就是让你为任何函数创建一个运算符。

我们假设你有一个用两个参数的函数f——比如Select，然后：

这个函数是用一个参数的函数，然后根据这个函数建立f[x,y]：

OperatorApplied允许一些编程，通常可以让你不用使用#和&等来插入纯函数。

最开始，OperatorApplied看上去像是一个非常抽象的“高阶”结构。但很快就变得自然了，而且在比如当你需要为某事提供一个函数时——比如设定一个选项，Outer的第一个参数等等——这个功能就会变得非常便利。

默认情况下，OperatorApplied[f][y]会创建一个应用于表达式的运算符，这也将会成为 f 的第一个参数。当你指定参数应该如何结合在一起的时候，有一个通用的格式：

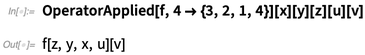
CurryApplied是OperatorApplied的一个纯变种，它会事先指定你可以预期到的参数的数量，然后（除非另有说明）这些参数将会以之前呈现的顺序进行使用。所以比如说，下个范例中可以预期函数有两个参数：

不用我说——既然这是一个纯构建，那么CurryApplied本身就会有一个运算符形式给出应该预期的参数数量：

在12.1版本中，我们还引入了另一个便利的副词：ReverseApplied。就像这个函数的名字说的一样，它使函数以其逆方向运行：

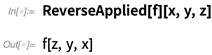
这在你指定排序函数的时候尤其便利：

所有这些符号函数式编程都强调了以结构式的方式思考符号表达式的重要性。另一个可以帮助这种思考方式的新函数是ExpressionGraph，它把表达式的树状结构（如TreeForm）变成了一个可以操控的实际图像：

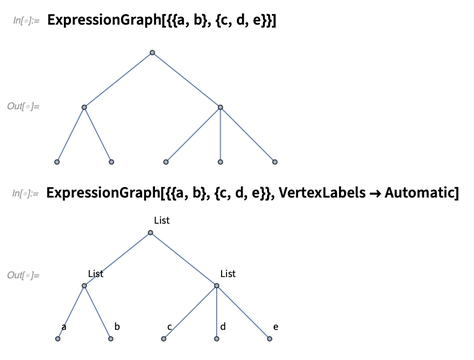
当我们在讨论编程的各种细节时，涉及到版本12.1的一个新功能是TimeRemaining，这个函数的作用，就像它名字所透露出来的，是用来告诉你还剩多少计算时间。所以比如说，在这里TimeConstrained显示计算应该被分配五秒钟的时间。但是在Pause用了一秒，所以只剩下不到四秒钟：

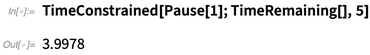
如果你在写复杂的代码时，这个函数可以帮助你知道你的计算还剩下多少时间，用来帮助你判断是否值得换一个不同的策略等。

现在我们可以证明苏格拉底不会永生

在使用Wolfram语言时重点通常是计算的结果是什么，而非为什么。但在11.3版本中，我们引入了FindEquationalProof，可以给出给定公理的证明。

AxiomaticTheory提供了一个标准公理系统合集。其中一个是群论的公理系统：

这个公理系统对于一般群论结果来说已经非常够用。比如说我们可以显示——即使公理只是断言 e 是右单位元——我们也有可能通过该公理证明出还存在一个左单位元。

下面这个数据集显示了这个自动生成证明系统的实际步骤。

但如果你想证明的是某个指定的有限群，那么这个内容已经在12.1中有所扩展。比如下例是一个四元数群，以默认符号给出：

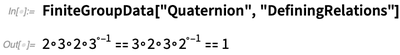
为了使用FindEquationProof中的这些公理，我们需要把他们的符号和我们用在群论公理的底层符号进行合并。在12.1中，你可以在AxiomaticTheory中直接进行这一操作：

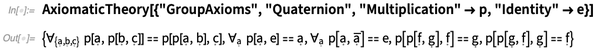
但对于大多数四元数的符号来说，我们还需要进一步指定：

但现在我们可以证明这些四元数的定理了。这个函数生成了一个54步的过程，说明了我们称为i 的生成器的四次幂是单位元：

除了做数学证明外，我们现在还可以使用12.1版本中的FindEquationProof来进行任意谓词的通用证明（或者更具体的说，叫做一阶逻辑）。以下是三段论中一个非常著名的范例，讨论人(man)与死(mortal)的结论。FindEquationProof给出了一个结论，苏格拉底会死。

我认为这个结论是有可能的，但是必须承认实际的证明过程有一点难读（在这个例子中有53步），因为证明过程中包括了到方程式逻辑的转换。

FindEquationProof可以自动证明很多内容。下面是Lewis Carroll给出的一个逻辑问题的解答，（在100步之内）说明婴儿没有能力管理鳄鱼：

为万物定位

Wolfram语言知道很多事情。其中一项就是地理。在12.1版本中，我们大幅提升和扩展了地理数据的资源（包括我们基于服务器的算法）。所以比如说，地图可查到的细节水平有大幅提升：

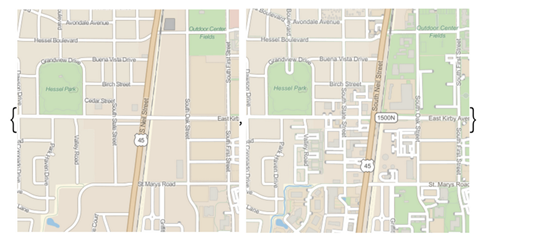
这些年来Wolfram语言的大地测量计算功能一直都很优秀。而且我们还有强大的可以计算各种欧几里得空间区域的计算型几何学。但由于地球不是平的，我们在12.1版本中一个主要的成就是把计算功能带到了地理空间，处理非平面区域。

这在几何上是一个很有趣的练习。我们有，比如美国领土形状的多边形地理坐标信息，是地球上的一个经纬度区域。但是对于我们的计算型几何功能来说，我们需要把它变成一个纯欧几里得。现在我们可以使用我们的大地测量功能将其嵌入到一个三维空间中。

现在我们可以计算美国领土形状区域的质心了：

地理位置的第三个元素是深度（以米表示），而且还可以反映美国领土多边形的曲率。这些信息可以直接被可视化：

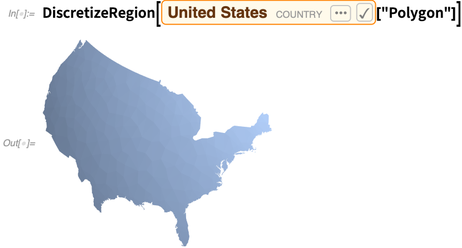
这是一个三维对象，所以我们可以旋转对象，以便更清晰地看到曲率的变化：

我们还可以用另外一种方式：使用地理位置并把它们投影到一个平面上，然后再进行计算。我知道格林兰岛如果使用不同的地图投影看起来会显示出不同的形状。下面是麦卡托投影的地区区域（以度的平方单位表示）：

下面是保积投影 (area-preserving projection) 的大小（以相同的单位表示）：

为了达到我们为万物定位的目标，12.1版本中还包括了GeoDensityPlot和GeoContourPlot。

知识库

每一天每一秒都有新的信息被存进Wolfram知识库，帮助WolframAlpha和Wolfram 语言变得更强大。为保证信息的正确且及时，我们付出了很多努力。但不仅于此，我们还将继续推进，以覆盖更多的领域，最终的目标是让世界上尽可能多的事物都能被计算。

我之前提过我们是如何构建一个新领域的计算型知识库的：数据结构的不同类型。我们已经覆盖了很多不同的新的领域。现在我举一个使用到不同数据结构的领域的例子：山羊品种。有看过我们直播设计回顾会议的人评论过，我一般会使用“山羊的内脏” 作为比喻（是因为突然想到巴比伦占星师从某种程度上来讲开创了我们现代科学的前身），因为具体的细节不方便透露给用户。但这并不是我们在12.1中拥有山羊的原因。

在近十年中，我们涉猎了小一百万个品种，我们在不断扩大这个范围，研究最近一次某个特定品种蛇类的牙齿数量可能在1800 年代某个时间点出现过。但我们还有一个项目是往深处挖掘这些与我们的用户（也就是人类）可能相关的品种——和其亚种。这就是为什么我们在12.1版本中涵盖了山羊品种（包括很多其他内容）的原因：

Wolfram语言和Mathematica所能覆盖的数学领域和计算发展是一条很长的路，但是我们这30年来一直想要实现的目标是让这个世界上尽可能多的内容都能被计算。其中一个我们深入开发的内容——并已经取得了很好的效果——是食物。我们已经涵盖成千上万种食物——成品包装的、区域性的、你能在菜单上看见的等等。在12.1中我们还加入了烹饪时间（和温度等等）作为可以计算的数据：

ExternalIdentifier、Wiki数据等等

书籍都有ISBN，化学品有CAS号，学术论文有DOI，电影有ISAN。世界充满了各种标准化的标识符。12.1版本中我们引入了新的符号构建ExternalIdentifier，可以提供引入外部有标识符的事物——然后将它们都链接起来——无论是在标识符之间，还是在我们会整合进Wolfram语言的实体和实体类型之间。

所以比如说，这里是如何用ISBN显示我的著作的：

目前我们支持46种外部标识符，而且在未来我们将覆盖更多更广的标识符类型。其中一个比较有代表性的例子是我们对 Wikidata 标识符的支持。这一功能帮助我们搭建内置知识库的结构，也帮助我们在诸如 SPARQL 支持方面的工作进展。

下面以我为例，查找我们的符号表达：

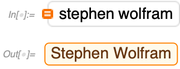
现在我们可以使用WikidataData函数获取我的WikidataID：

下面查找我属于哪一类Wikidata类别：

并不是很深入的研究结果，但就我所知这个结果是正确的。

在过去数年中Wikidata收纳了很多数据。有一些数据很好，有一些则不然。但在12.1版本的WikidataData中，你可以系统性的研究函数里有什么。

举一个在可预见的未来内我们不太可能会策划的一个内容：著名骗局（hoax）。首先我们使用WikidataSearch查找骗局：

将鼠标悬停在每一项上方以查看更细节的内容：

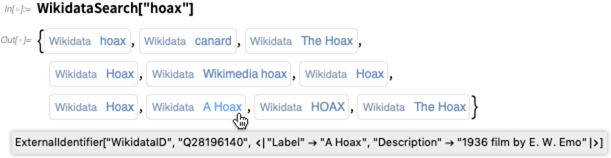
现在看起来，第一项似乎是骗局的种类。所以现在我们以此为例，做一个数据组看一看这个实体类别中都有什么信息：

我们可以使用Wikidata ExternalIdentifier来表示地理位置，然后查看这些骗局的位置。结果并没有给出太多的地理位置，而且我有一点怀疑那个在Null岛的结果是如何给出的（可能这也是一个骗局？）：

另一个范例，在语义上比上一个范例更加精细，我们现在来查看哲学研究内容的反义是什么，并把得到的结果结合起来：

那是什么分子？化学计算上的进展

假设你在一篇论文上获取了一个分子结构图的图像。你现在要如何把这个分子转换成可计算的格式？在12.1中，你只需要一个函数MoleculeRecognize：

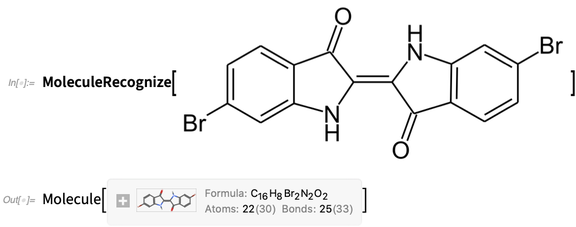
这个函数有一点像TextRecognize，只是对象是分子。该函数给出的是Wolfram语言中分子的符号表示。所以比如说，接下来你可以生成一个三维结构：

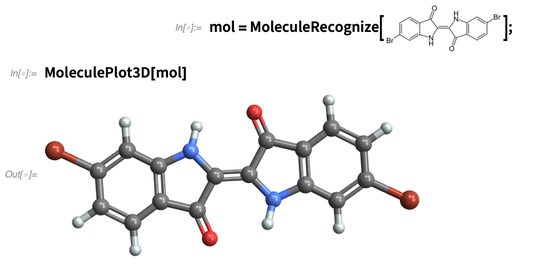
或者你可以计算这个结构扭转角的分布：

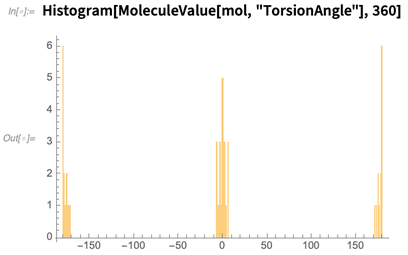
你还可以链接到外部标识符

但是MoleculeRecognize真正有用的地方在于，它可以以编程的方式使用。从论文中获取化学品结构图像，并对其进行分子识别——然后检查得出的分子是否等价，或者用它们的三维结构创建一个文字云：

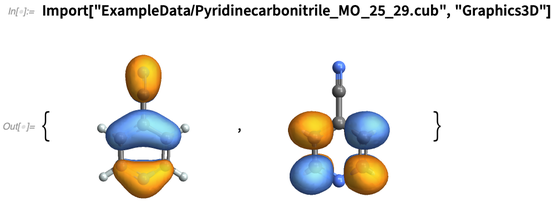
除此之外，12.1版本中还有一个新内容——也是一个非常重要的内容——是可以导入分子轨道数据的功能：

让数据资源库变得更简单

我们在2019年6月发布了Wolfram函数资源库，已经包括了1146个函数。函数资源库的一大创新是其流线型的操作过程，包括可应用于公共函数资源库，和在单一机器或云端以个人部署为目的的新函数提交。

在12.1版本中，我们为数据资源库引入了一个新的流线型提交机制。即进行文件> 新建>资源库项目>数据资源库项目：

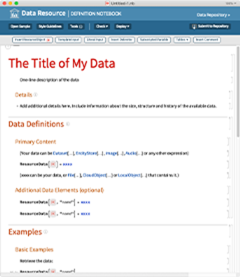
然后如果你获取了，比如说，一个数据组，你可以把它插入到笔记本中，然后再添加范例（还能使用“插入ResourceObject” 按钮插入你所创建对象的参考内容）。完成了这些步骤后，点击Deploy，然后你就可以在本地部署，或在云端私人或公共部署。检查工作也会同时自动完成（如果有任何错误一般你会收到一个如何修正错误的建议）。

我的目标是建立一个简单的可以在几分钟之内创建的数据资源库，我觉得我们用流线型和自动化工作流程已经达到了这一目的。