关键词：概率、神经网络

关注过Mathematica Stack Exchange（我强烈推荐给各位Wolfram语言的用户）的读者们可能最近看过这篇博文内容了，在那篇博文里我展示了一个我所编写的函数，可以使得贝叶斯线性回归的操作更加简单。在完成了那个函数之后，我一直在使用这个函数，以更好地了解这个函数能做什么，并和那些使用常规拟合代数如Fit使用的函数进行比较。在这篇博文中，我不想说太多技术方面的问题（想要了解更多贝叶斯神经网络回归的内容请参见我前一篇博文 - https://wolfr.am/GMmXoLta），而想着重贝叶斯回归的实际应用和解释，并分享一些你可以从中得到的意想不到的结果。

01 准备工作

获取我的BayesianLinearRegression (https://wolfr.am/GMn9Di7w)函数最简单的方法是参考我上传到Wolfram Function Repository 的内容。如想要使用本博文中的代码范例，你可以计算下列代码，这段代码为该函数创建了一个快捷方式。

你也可以访问GitHub repository并参照安装说明，使用以下代码加载BayesianInference安装包：

或者，你也可以通过计算 BayesianLinearRegression 的独立源文件（https://wolfr.am/GMngf5Uj）的方式获取该函数，只是如果你没有完整的BayesianInference安装包的话，你可能无法使用我后面会用到的函数regressionPlot1D。该函数的定义在BayesianVisualisations.wl（https://wolfr.am/GMnlzNkh）文件中。

02 回到基础

我现在要做一些对有数据拟合背景的大部分人都非常熟悉的事情：多项式回归。我可以用更复杂的例子，但是我发现用贝叶斯函数做数据拟合，即使是在如多项式回归这样简单的范例上也能延伸出很多新的可能性，所以其实这是一个非常好的演示范例。

下面我用了一组有直线关系趋势的数据，但同时也留下了一些问题：

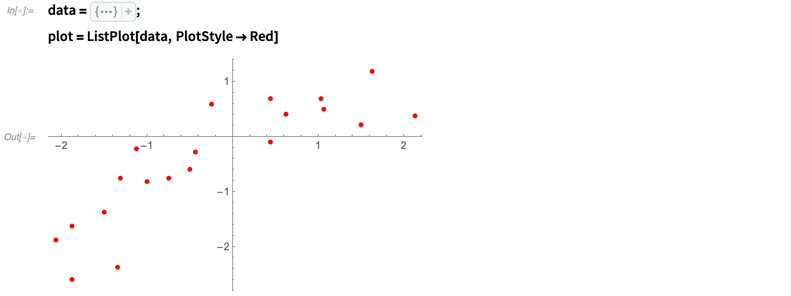
现在我们从第一件事情做起：为数据拟合一条直线。具体来说，我会拟合模型y=a+bx+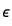，其中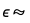NormalDistribution[0,σ]. BayesianLinearRegression和LinearModelFit 使用相同的语法，但是它还能返回一个包括所有与该拟合相关信息的关联关系：

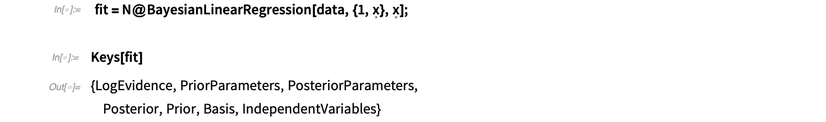
我会着重解释后验分布和log-evidence。Log-evidence是一个说明模型对数据组拟合程度的数字。

这个值是好是坏？我们现在还不好说：这只是一个与对相同数据进行拟合的其他模型对比的一个值。我后面会在说到贝叶斯奥卡姆剃刀（Bayesian Occam’s razor）部分的时候说模型比较，但是现在我们先仔细看一看我们刚才计算出的先行拟合。这个拟合的关联关系中有一个关键称为“后验（Posterior）”, 其中包括了一个很有用的概率分布的数字：

在贝叶斯推断中，“后验（posterior）”这个词指的是在观察数据后的认知状态（与“先验（prior）相对”指的是还不了解数据的状态。回归参数的后验分布可以告诉我们参数a和b是如何被数据约束的。可视化这一过程最好的方式是通过ContourPlot来实现：

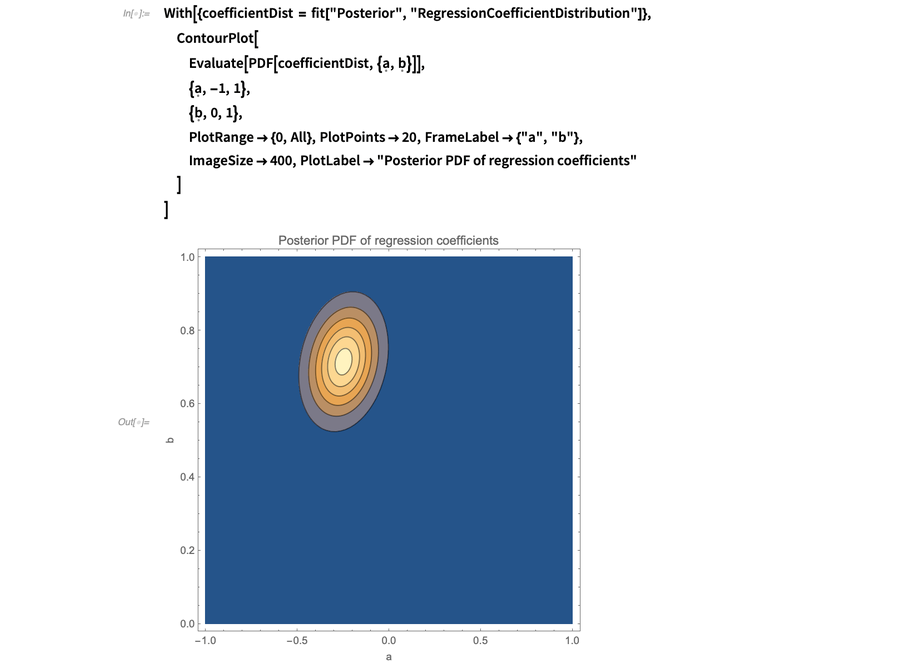
乍看之下，这看起来有点奇怪。a和b为什么互相关联？其中一种思考方式是看当迫使这两个系数其中一个变化时，拟合会如何变化。例如，可以固定a和b并用FindFit尝试找到可以拟合数据的最佳值。下图说明了这个思考尝试：

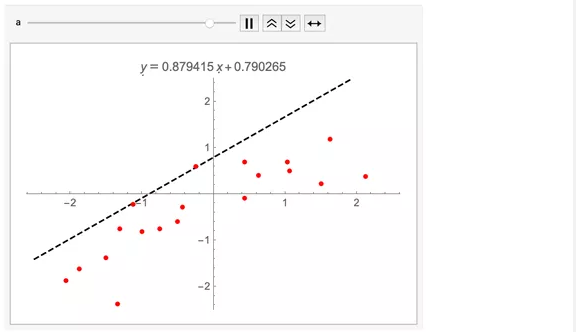
可以本能判断a与b之间确实相关，因为这些点的质量中心轻微偏向了原点的左下方：

这说明当a增加，b也需要增加，这样才能符合点群的质量中心。这里我略微更向下移了一点，这个效应就更加明显了：

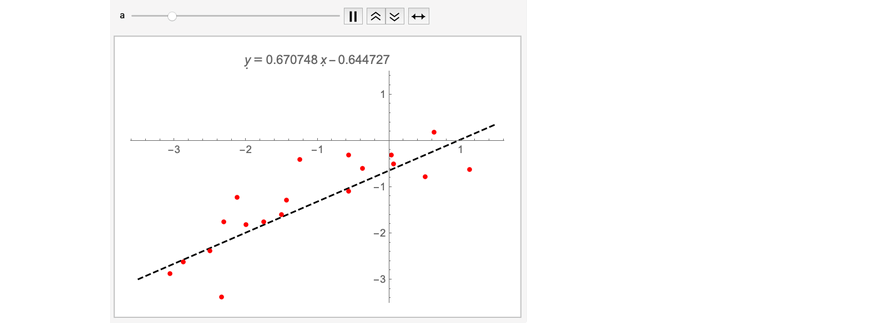
另一个思考和上的后验分布的方法是将拟合想象成由无限条直线组成，在平面上随机绘制且权重由其对数据的拟合程度决定。计算该权重就是贝叶斯推断所讨论的内容。在下图中，我用RandomVariate绘制了从后验来的很多直线。当调低每条直线的透明度后，你可以看到直线趋于集中的区域：

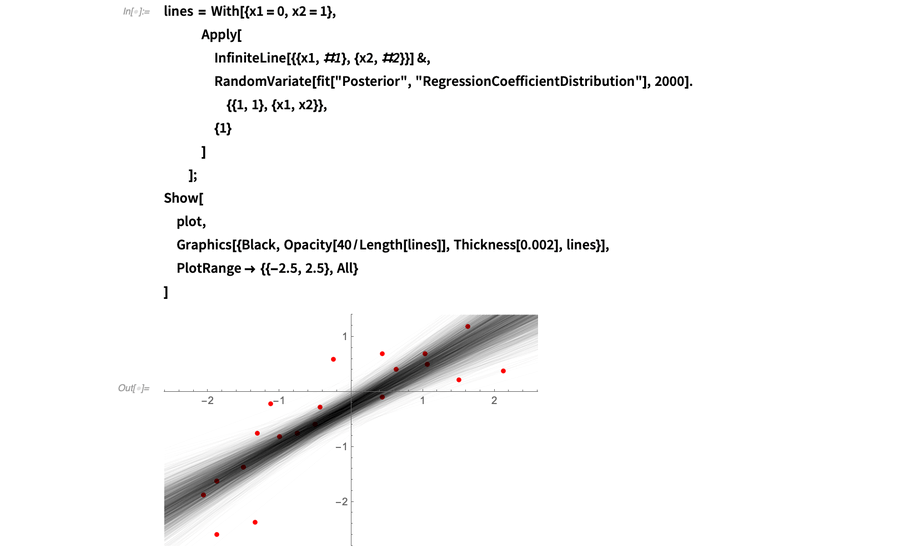
我喜欢把这个直线群的分布称为“底层值分布”，这也是拟合会返回的分布之一。可以通过InverseCDF便捷地计算分布的分位数并绘制该分布。在下个例子中，我绘制了5%、50%和95%分位数，意味着你会期待90%的直线会落在阴影区域内：

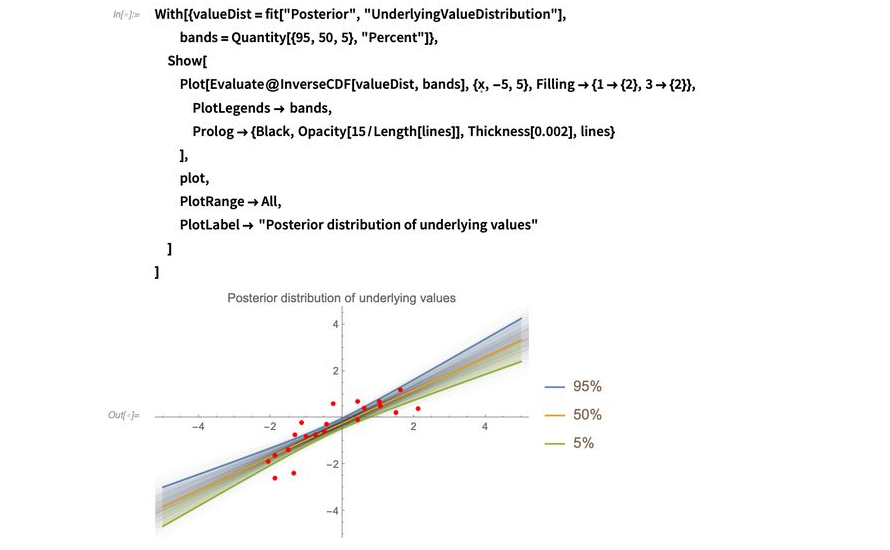
BayesianLinearRegression也可以计算误差项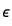的标准差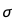， 而且就像回归系数a和b一样，它有自己的分布。方差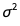遵循一个InverseGammaDistribution， 所以可以使用TransformedDistribution获取的分布：

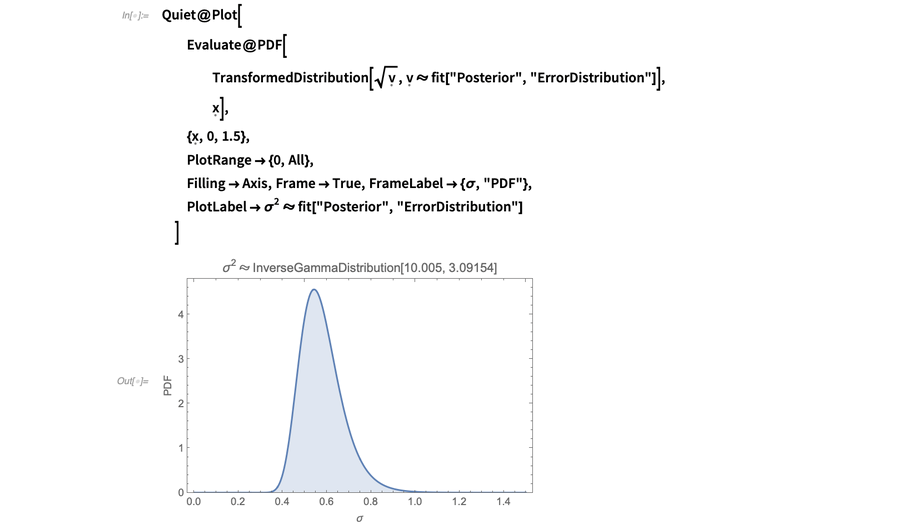
所以简单来说，后验误差项的分布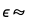所以简单来说，后验误差项的分布是NormalDistribution[0, σ], 其中 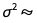InverseGammaDistribution[10.005,3.09154]。我们可以用ParameterMixtureDistribution来计算这个分布：所以简单来说，后验误差项的分布是NormalDistribution[0, σ], 其中InverseGammaDistribution[10.005,3.09154]。我们可以用ParameterMixtureDistribution来计算这个分布：是NormalDistribution[0, σ], 其中InverseGammaDistribution[10.005,3.09154]。我们可以用ParameterMixtureDistribution来计算这个分布：

03 不确定的不确定度

先说明一下：模型的不确定度是不确定的，这个观点我最开始也有点难以想通。为了让情况再复杂一点，我前面提到的所有线条都有和a和b关联的误差条。因此如果你想要使用这个模型做一个预测，你需要考虑无数带有无限数量误差条的趋势线。这要求考虑很多不确定性！

用这种方式思考回归问题就能明白为什么贝叶斯推断是一个包含了很多复杂几分的艰巨任务。但是对于线性回归，我们很幸运，因为可以使用符号来解决所有的积分并在无限中继续前进。这也是为什么科学家和工程师这么喜欢线性数学的原因之一：所有事情都可以用很漂亮的公式来处理。

能告诉你可以预期在何处找到未来的数据（考虑到之前提到的所有不确定）的分布称为后验预测分布（posterior predictive distribution）。所以刚才拟合的数据长这样：

下面我就用Git仓库中的函数regressionPlot1D来绘制这个分布，这也是我刚才展示的底层值绘图的简便方法。 我还加上了一个当你在做预测模型的“点估算（point estimate）”时会得到的分布。 这就意味着你从后验中获得了a、b和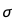的最佳值，并假设这些值是完全确定的情况下使用这些值来绘制 y=a+bx+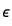。 点估算可以帮助让结果更加可控，因为概率分布是很难使用的，但是把分布减少到单个的值也就意味着舍弃了信息。这里我使用了Mean（期望值）来减少单个值的分布，当然你也可以使用其他集中性的度量如中位数或众数：

所以这就说到了用一条直线拟合这些点。但是数据的形状说明也许二次回归拟合会更合适（当然我使用这个例子就是为了说明这一点），所以现在我们可以展示贝叶斯模型对比是怎么工作的了。我准备用最高5阶的多项式来拟合数据，每一个多项式代表一个可以解释这些数据的模型。从这些数据所有可能解释中，我要选择最好的一个。

04 贝叶斯奥卡姆剃刀定律

在贝叶斯推断中，模型的概率分布和回归系数的a、b和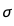的分布一样。模型的后验概率取决于两个因素：

■ 一个被称为证据或边缘似然的量。这个量衡量的是当考虑到回归参数如a、b和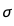的不确定度时模型对数据的拟合程度。BayesianLinearRegression将这个量返回为“LogEvidence”，数字越高，拟合得越好。该证据由于一个时常被称为贝叶斯奥卡姆剃刀定律的效应会自动考虑模型的复杂程度（可参见David MacKay的著作中第28章的范例

■ 模型的先验概率

在看到数据前，通常你只需要考虑所有模型的可能性是相等的。但是有时候，你会对数据有很多先验信息，知道数据是由某个模型生成的，且你只想接收那些明显能证明现有模型比其他模型更好的结论是错误的证据。

比如，如果数据来源于一个通过以电压作为参数的标准电阻函数测量的电流，测量数据会有噪声（且有可能偏误），那我会觉得欧姆定律适用在这里，并且用一条直线拟合这些数据是正确的。这更像是一点噪声可能会让数据看起来像符合二次拟合，而欧姆定律好像突然在实验中不对了。在这种情况下，我会给欧姆定律设定一个接近于1的先验概率，并把剩余的那一点点概率分配在其他待考虑的模型中。这符合由Dennis Lindley提出的一个叫Cromwell’s rule的原理：

“对月亮是新鲜乳酪做的这个观点保留一点点可能性，哪怕是百万分之一，但还是把它留在那里，否则那些从月亮回来的带着新鲜乳酪的宇航员们可能会把你堵得水泄不通。“

那么现在让我们来看看不同多项式的拟合看上去如何，并且它们的证据都是什么：

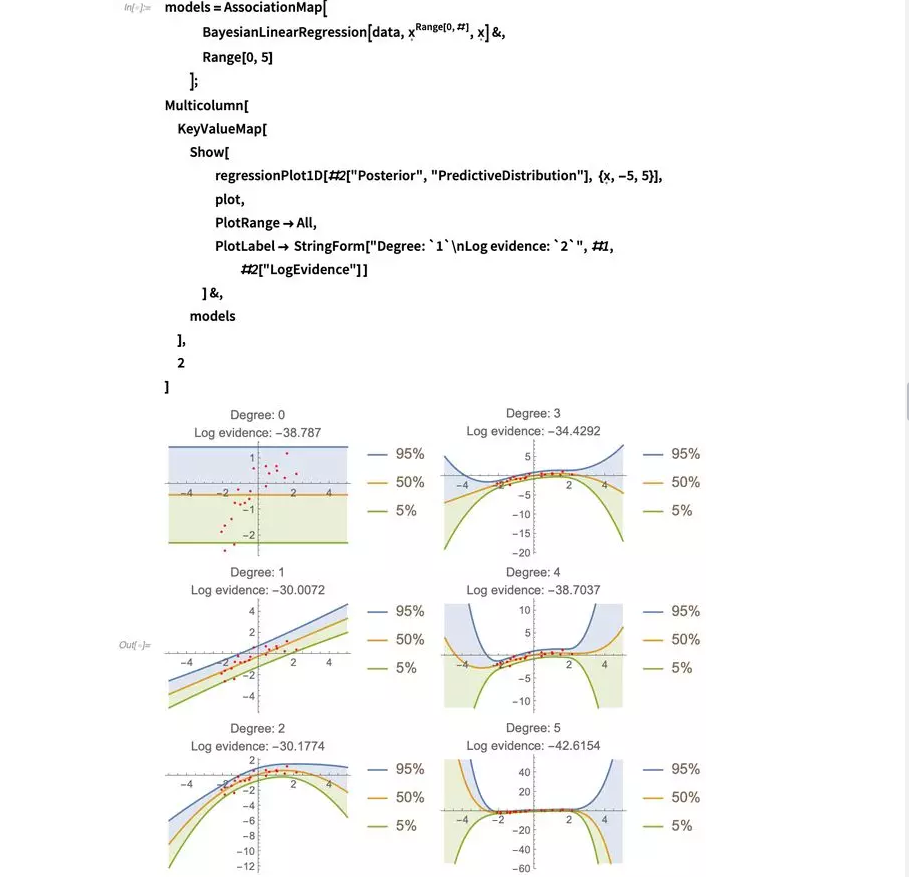
你可以看到，一阶和二阶拟合在最佳模型的竞争上很相近。如果我们假设所有模型的先验概率一样，那么我们可以通过对log-evidence取幂并将其正态化来计算拟合的相对概率。我们可以借用神经网络框架中的SoftmaxLayer来进行这个操作。

在这个表格中，我按照概率对模型进行了分类，并把它们累加，然后你就能很容易地看出从上到下总概率是多少。记住这些概率只意味着我们现在研究的这个微观世界：当我增加更多的模型那一刻起，所有概率都可能会改变。在贝叶斯推断中，你可以只比较你想要首先构想的那几个模型：不存在可以在完全客观的角度上告诉你数据拟合好坏的普适度量。你能希望的只是在你所考虑的模型群中找到最好的模型，因为你没有考虑到的模型是无法进行对比的。

05 小插曲：和LinealModelFit作比较

到现在，可以把用BayesianLinearRegression做的拟合和用LinearModelFit做的拟合进行一个对比，这同时也展示了一些拟合优度的度量：

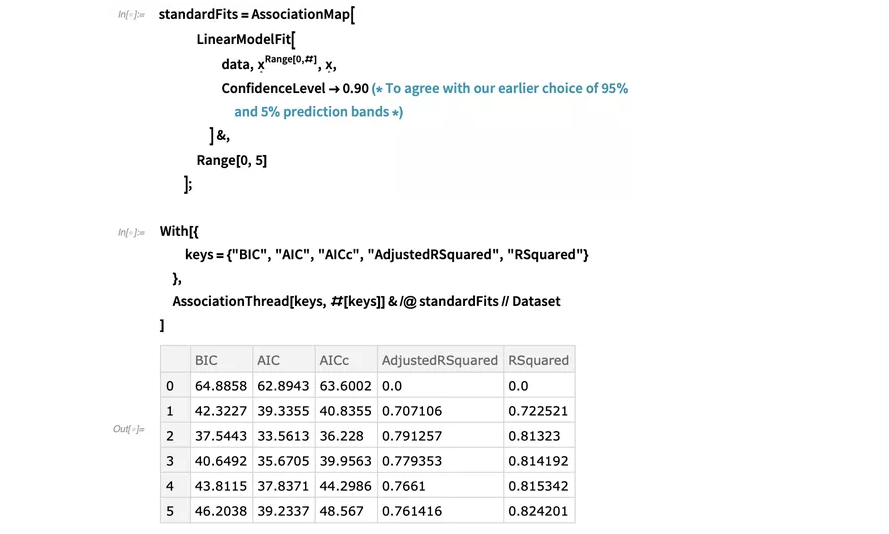
如预料一样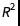， 度量不受模型复杂程度影响， 随模型阶数的升高而上升。而其他所有度量似乎更倾向于二阶模型：记住越好的模型，Bayesian information criterion（贝叶斯信息标准）（或称为BIC，是负log-evidence的一个近似量） 、Akaike information criterion（赤池信息标准）(AIC) 和AIC校正值都越高。 对修正 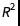而言，有最高值的模型最优。我们再比较一下从LinearModelFit和贝叶斯方法中得到的二阶模型预测区间：

你可以看到，从LinearModelFit得到的置信区间会比后验预测区间更宽一些（所以也会更悲观一些）。产生这个差异的一个主要原因是贝叶斯预测考虑了所有后验分布中模型参数的相关性，并把该相关性应用于预测使得预测区间可以缩小一点。另一个解释这个结果的方式是，贝叶斯分析在计算预测区间时不会提前舍弃信息因为它会完全保留所有中间分布。这个效应在数据变少时会更加显著，如同下图说明的一样（如果你对贝叶斯先验在这个范例中扮演的角色有所怀疑，我建议你可以自己尝试一下逐渐减少先验信息然后对比结果）：

06 整合结论

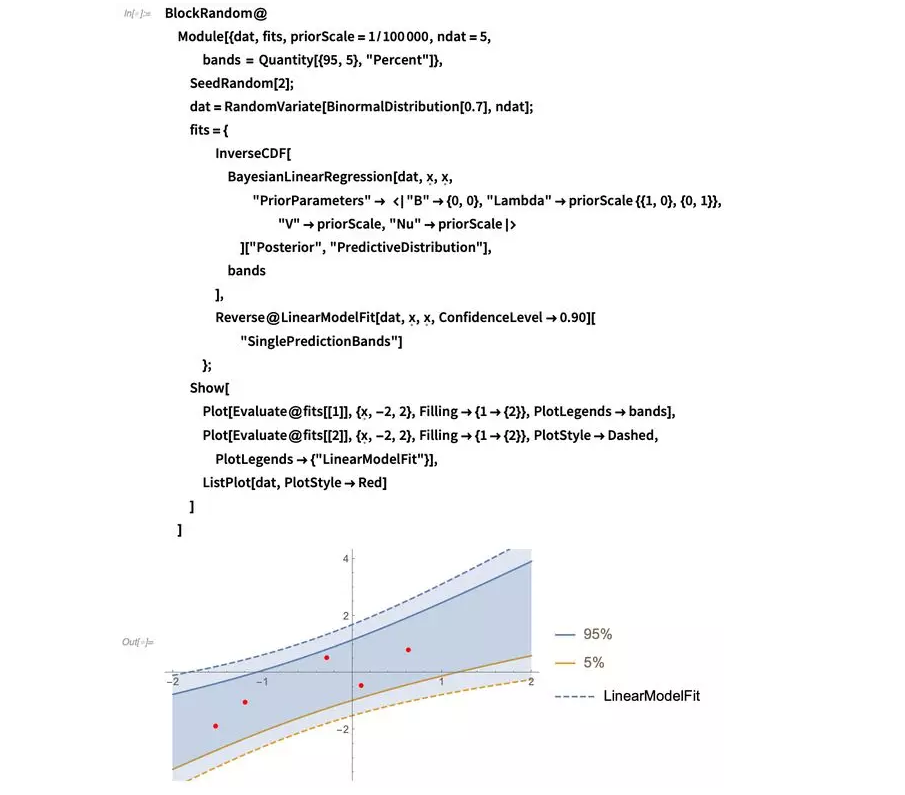
所以现在我们有一些多项式模型，之中的两个在竞争最优模型，但没有明显的胜出者。所以我们应该选择哪一个？贝叶斯简单地回答了这个问题：为什么不保留这两个？ 我们仍然在研究一个概率论的观点：答案可能就在这两个模型中间的某个地方，没有必要明确哪个选择是最好的。 选择一个模型也是点估算的一种形式，我们之前看到了点估算会舍弃一些可能有用的信息。但是我们还能选择像之前一样通过将a、b和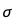所有可能的值取平均并把直线拟合进数据中，来把这个差异分离。函数MixtureDistribution在这里会非常有用，它可以将不同的后验预测合并进一个新的分布。甚至不需要仅仅考虑一阶和二阶模型：我们可以按照权重合并所有模型：

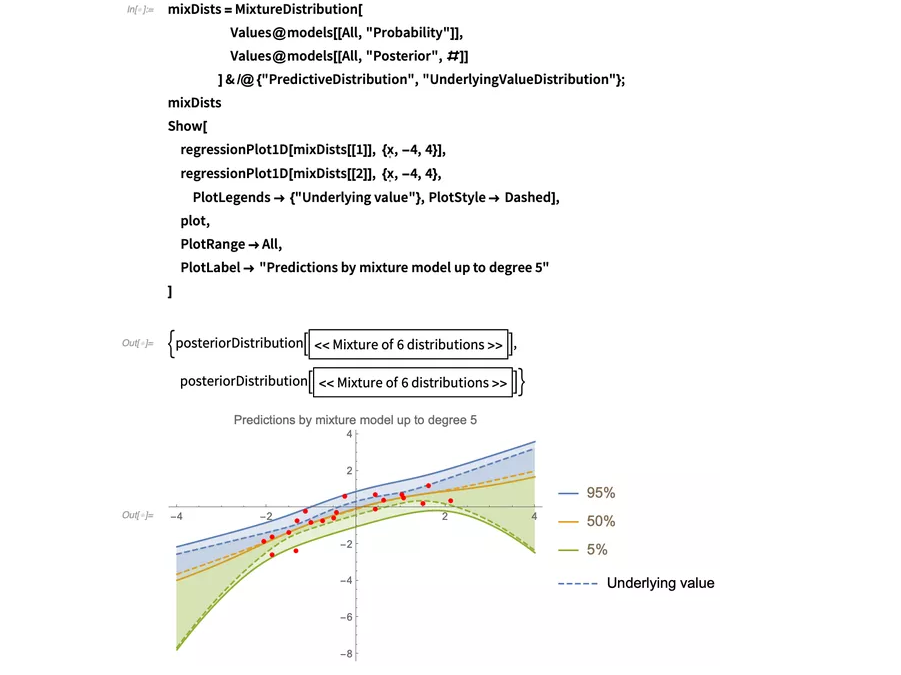
（注意BayesianInference安装包中的MixtureDistribution的自定义压缩格式。）底层值区间把很好的突出了模型结合。

那为什么我们要停在这里？多项式世界中还有更多的模型可以探索，所以我们稍微延伸一点。比如，为什么不尝试一下像 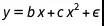的拟合（即：没有常量偏移）？有最高为5阶的63个模型可以尝试：

下面的函数可以让模型拟合过程更简便快捷：

拟合所有最高5阶的多项式，并查看最优的10个拟合：

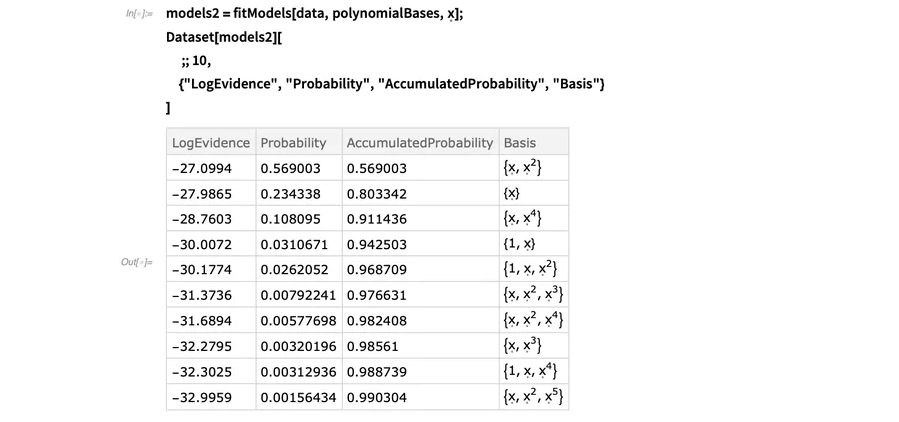
我现在又可以计算预测区间了，但确实没有必要在这个整合模型中包含所有模型，因为只有少数模型的权重会很高。 为了更好地可以处理这个分布，我会为总概率质量舍弃一些可能性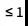%的模型：

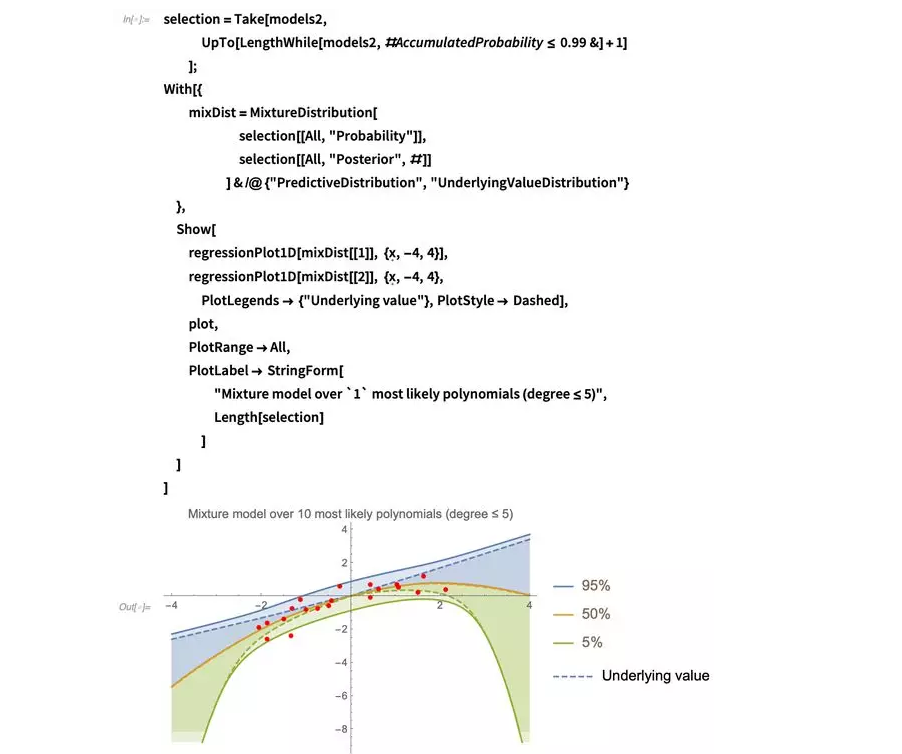
很有意思的事情是，我们发现没有常数偏移的模型明显会更优，他们能给出在原点附近范围非常窄的底层值估算。外推区间也会比之前更宽，但这只是一个关于外推的危险信号：如果我们确实相信所有多项式都是解释这些数据的同等有力的竞争者，那么较宽的外推区间就是这个假设的一个很自然的结果，因为毕竟可以解释数据的可能模型太多。这还是优于另一个选项：设想一下你可以非常精确地做外推，但之后可能基于这个错误的精确性做出一些重要决定，最后被证明结果是错误的。

另外，思考我们现在了解的我们数据拟合的基础函数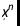的回归系数也很有意思。在下面的代码中，我计算了回归系数分布每个部分的MarginalDistribution并可视化它们的置信区间：

把这个置信区间与你用单个5阶多项式而非63个不同的多项式拟合时得到的置信区间比较，后者明显包含的信息更少：

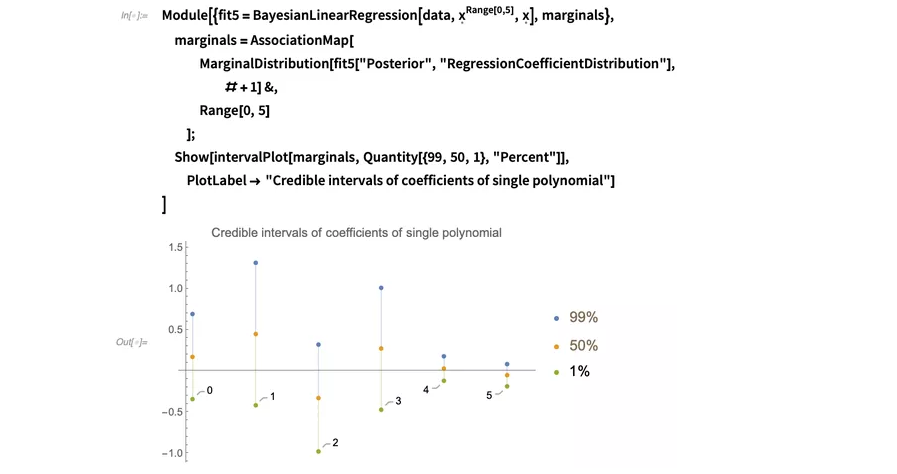
第一个图显示，我们可以确定多项式中的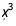和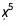是0， 且我们现在已经知道了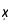、 和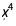项的符号，但我们只能通过尝试所有可能的多项式，把它们相互比较并最终得出结论。

这个过程也与让拟合项消失的其他常用方法不同，称为LASSOFitRegularization：

06 整合结论

我希望这篇贝叶斯回归的内容会对你有些许帮助。如果你还对BayesianLinearRegression使用的底层数学感兴趣的话，你可以查阅维基百科的贝叶斯线性回归、贝叶斯多元回归和共轭先验。

用Wolfram函数存储库中的BayesianLinearRegression或下载BayesianInference 安装包，可以尝试怎么用贝叶斯回归更好的处理你自己的数据。我很期待看到大家以不同的方式使用BayesianLinearRegression，并在Wolfram 社区上分享你的结果和小建议！