解决方案

Mathematica 12 为偏微分方程(PDE)的符号和数值求解提供了强大的功能。本文将重点介绍版本12中全新推出的基于有限元方法(FEM)的非线性PDE求解器。首先简要回顾用于求解 PDE 的 Wolfram 语言基本语法,包括如何指定狄利克雷和诺伊曼边界条件;随后我们将通过一个具体的非线性问题,说明 Mathematica 12的 FEM 求解过程。最后,我们将展示一些物理和化学实例,如Gray-Scott模型和与时间相关的纳维-斯托克斯方程。更多信息可以在 Wolfram 语言教程"有限元编程"中找到,本文大部分内容都以此为基础
Wolfram Research 的旗舰产品 Mathematica 通过5000多种内置函数驱动着 Wolfram 语言。在作为数学建模和分析基础的常/偏微分方程领域,Mathematica 12 具有功能强大的求解器来对其进行符号或数值求解。最近,基于有限元法的数值求解函数得到显著增强,并有望求解任意区域上的PDE并获得特征值/特征函数。在此,我们将着重介绍 FEM 在最新版本12中对非线性偏微分方程的求解,并通过实例介绍在实际问题中的应用流程。使用有限元方法求解非线性 PDE 的详细过程和代码信息向公众开放,请参见Wolfram 语言教程"有限元编程"。
在 Wolfram 语言中,对微分方程进行数值求解的函数有两个:NDSolve 和NDSolveValue。两者仅在输出格式上有细微差异,内部处理则完全一致。因此,在下面的文本表述中,将用简短的 "NDSolve",而将便于输出的"NDSolveValue" 用于代码范例中。若要在 Mathematica 上使用 FEM,首先加载软件包:

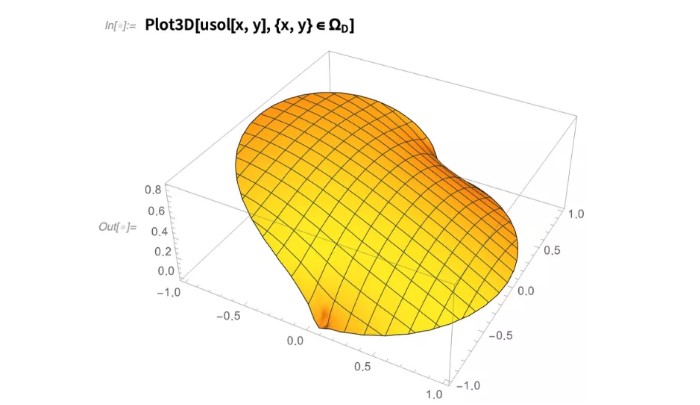
然后,我们要做的就是给 NDSolve 提供一个 PDE、区域和初始及边界条件。以在单位圆上的泊松方程 –∇2u = 1 为例,如果以在 x>=0 上 u=0 作为边界条件:

所得出解的图形为 :
目前,在 NDSolve 中适用于有限元法的偏微分方程式必须具有以下形式:
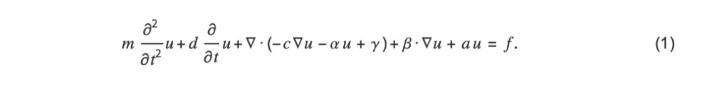
此处,待求解的因变量 u 在 Rn上为一维函数时,m、d、a、f 为标量,α、γ 和 β 为 n 维向量,c 为 n*n 矩阵。此外,c、a、f、α、γ 和 β 可依赖 t、x ∈ Rn、u、∇u 等,但 m 和 d 仅对 x 有依赖性。对于多个因变量 u ∈ Rd建立联立方程式时,方程式 (1) 中,γ 和 f 为 d 维向量,其他系数是向量分量的矩阵。但是,当进行系数矩阵或向量 u 的运算时,微分运算符会被矩阵/向量的各个分量内的运算所继承,例如,∇(u1, …, ud)T = (∇u1, …, ∇ud)T 和
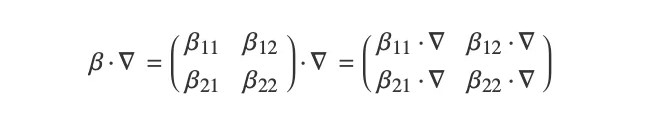
等等。
从自然科学到工程应用的多数 PDE 都是 (1) 的特例。例如,波动方程是除 m 和 c 以外的系数都为 0 时的情况,且表示不可压缩流体的速度以及压力场 u = (v, p)T ∈ R4 的 Navier–Stokes 方程式
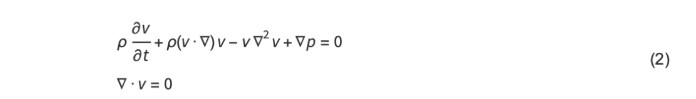
可用方程式 (1) 的形式表示。
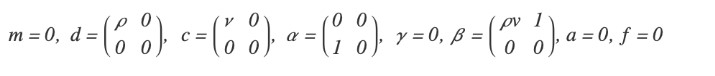
下面,我们考虑的问题将暂时与时间无关,并处理与空间维数有关的有限元法.与时间有关的问题将在第 3 节末尾作简要说明,并且在 4.3 和 4.4 节中给出范例。
重要的是,为了判断 FEM 是否适用,提供给 NDSolve 的方程应视为方程式 (1) 的形式 ("Coefficient Form"),包括各个系数的依赖性。举一个简单的例子,

该式相当于方程式(1) 中 c = –∇u, f = –4,并且将其他系数设置为 0 的情况。但作为提供给 NDSolve 的 PDE 进行输入时,
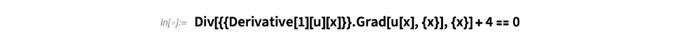
PDE 则在 NDSolve 开始处理前被计算,结果 2u´ (x)u´´ (x) 被视为方程式 (1) 的第一项.由于这并非是方程式 (1) 中 Coefficient Form 的形式,不能用 FEM 求解(u´´(x) 被视为 u´(x) 的系数,造成系数依赖于二阶导数函数的结果)。为保持方程式 (1) 的形式不变提供给 NDSolve,需要使用 Inactive 或者 Inactivate,
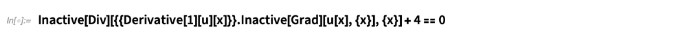
如上所示,保留对 ∇ 的计算即可。
您可以指定任何维数的任何区域。如果是像上述泊松方程示例那样的简单的图形,则可以通过 Disk 和 Polygon 的组合来创建;如果它是由等式和不等式表示的区域,则可以使用 ParametricRegion、 ImplicitRegion 等。此外,还可以通过 ImageMesh将由照片生成的图像转换成可供 NDSolve 使用的区域数据。
直接在边界 ∂Ω 上给出函数值的狄里克雷边界条件:

如上所示,只需用 PDE 指定即可。此处 bc 是给出边界值的函数,predicate是 f(x,y)=bc 需要满足的边界。如果仅将 predicate 设置为 True,则将指定整个∂Ω。
广义诺伊曼边界条件(洛平边界条件)由 NeumannValue 指定。洛平边界条件以下列形式定义了垂直向外穿透边界的通量分量:

为 ∂Ω 上的外向法线(单位)向量,右侧的 g–qu 是由用户给定的值。但请注意,NeumannValue 与 DirichletCondition 的指定方法不同。这是因为在有限元逼近中,PDE 乘以测试函数 ϕ 并积分到区域 Ω 中以获得弱形式。在等式(1)的第一项 ϕ 上积分,
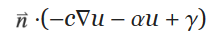 项则变为:
项则变为:
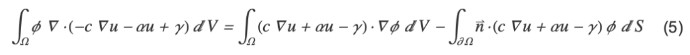
在边界 ∂Ω 上积分的被积函数刚好与在洛平边界条件应指定的值相对应。因此,通过用g–qu 的积分代替此项,NDSolve 则可正确处理该边界条件。
例如,在区域 u(x,y) = 0, x ≥ 1/2 中,对于单位圆边界 x ≤ 0,指定
·∇u = xy2的狄利克雷条件和诺伊曼条件,求解拉普拉斯方程 –∇2u = 0:

(在这种情况下,PDE 被明确识别为 Coefficient Form,因此不必将微分运算符设置为 Inactive,但也可以使用 Inactive[Div], Inactive[Grad]。)
Div 前的负号是为了让等式(1) 中的 c 成为 1,从而让诺伊曼条件
·c∇u = ·∇u = xy2 可直接输入 NeumannValue。绘制解的图形:
需要注意的是,由于 NeumannValue 是根据方程(1) 的 PDE 以方程 (4) 的形式确定的,因此可能需要"手动"调整诺伊曼条件。例如,对于泊松方程 –∇2u + 1/5 = 0,同时指定诺伊曼条件·∇u = xy2(x ≥ 1/2) 和狄利克雷条件 u(x,y) = 0(x ≤ 0),如果用于NDSolve 的 PDE 本身为 –5 ∇2u + 1 = 0,则 NDSolve 的公式 (1) 中认定 c = 5,与 ·c∇u 对应的 NeumannValue 必须为 5xy2。看起来似乎很明显,但需要注意的是,与狄利克雷条件不同,诺伊曼(洛平)条件并非独立于 PDE 而指定。–∇2u + 1/5 = 0 和 –5 ∇2u + 1 = 0 的情况如下所示。
如果输入式为 –∇2u + 1/5 == 0,则:
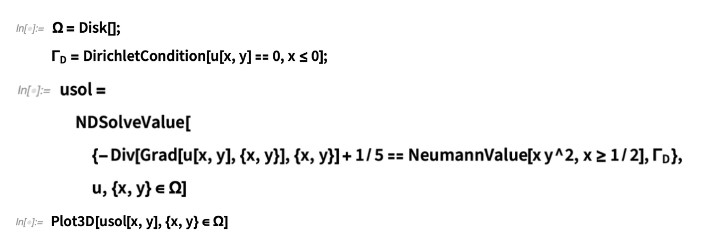
如果输入式为 –5 ∇2u + 1 == 0,则:

对于洛平条件 3u + ∇u = xy2 的情况也是如此,对于 NDSolve 内的 PDE,如果左侧为–∇2u+1/5,则右侧为 5*NeumannValue[1/2*x*y2 – 3/2*u[x, y], x≥1/2]。
为了应用 FEM,需要在目标区域中生成网格,在此不做深入讨论。对于有兴趣的读者,在此介绍几个简单工具供了解:Triangle 和 TetGen(链接见文末)。前者用于生成二维区域,后者用于生成三维区域。Triangle 可进行 Delaunay 三角剖分、约束 Delaunay 三角剖分(constrained Delaunay triangulation) 和限定Delaunay三角剖分(conforming Delaunay triangulation),TetGen 可以在三维区域中生成四面体网格,例如约束 Delaunay 四面体化和边界符合Delaunay 网格。Wolfram 语言将在需要时自动使用,但您也可以对其进行自定义灵活使用。有关 Triangle 的详情请参照 [4.1] 节,TetGen 的相关说明请参见 [4.2] 节。
在线性 PDE 的情况下,联立线性方程组是从 PDE 的弱形式到离散化来求解的,但这也用于求解非线性 PDE。以下为基本流程:
1、在成为种子的候选解附近线性化非线性PDE
2、对线性化方程进行离散化求解
3、如果种子和所获得的解的差异在允许的误差内,则结束
4、使用获得的解作为新种子,返回到第1步的线性化工作
也就是说,它遵循的过程与用 Newton-Raphson 方法求解非线性代数方程式的过程相同。在上面提到的 Wolfram 文档教程有详细介绍,以下为简单介绍。
首先,如果我们删除与公式(1) 的时间导数相关的部分,则有
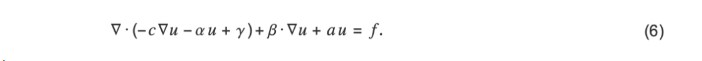
若将,

则变为以下简单形式:

尽管将非线性 PDE 进行线性化,与求 1 个变量的非线性方程组的数值解相同,将任意函数 u0 作为种子,由此渐进逼近使 ∇2·Γ (u∗) – F (u∗) = 0 的真正解 u∗,令 u∗与 u0之间的差为 r = u∗ – u0,则得出:
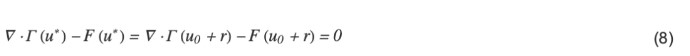
将 Γ、F 在 u0 周围通过泰勒展开,忽略 O(r2) 的高阶项,则得出:

对 Γ ' 或 F ' 的微分求导,可通过计算 ∂Γ/∂∇u、∂Γ/∂u、∂F/∂∇u、∂F/∂u 等得出。当它们在 u0 处求值时,等式(9) 成为每个离散点(节点)上 u 的联立线性方程。在这里,通过同时联立的初始条件和边界条件,从而形成一个封闭的联立方程并且得出 r。
种子 u0 默认为 u(x) = 0, ∀ x ∈ Ω,是 NDSolve 的一个选项,例如,可指定为 InitialSeeding→{u[x,y]==x+Exp[-Abs[y]]} 考虑到线性化的渐近解可能导致意想不到的局部解,提供与问题相符的好种子也是有用的。另外,从等式(13)计算残差 r 时,左侧出现的雅可比矩阵 ∇·Γ '(u0) – F '(u0) 的计算量很大,这极大地影响了整体计算时间。因此,在 Wolfram 语言中,当应用非线性 FEM 时,将使用仿射协变牛顿法(Affine Covariant Newton)代替 Newton-Raphson 法,并且在允许的范围内可以重复使用上一步中的雅可比法。从而显著减少雅可比的计算次数。
对于时间相关的积分,可以通过离散化空间维度以获得方程组(矩阵),然后将其作为关于时间的常微分方程,从而应用各种计算方法。直线数值法 (Method of lines)等[5],在某些情况下,也可以将 FEM 应用于时间维度。
电流周围会产生磁场 。当电流以类似电动机的配置流过线圈时,会产生什么样的磁场分布呢?对于非线性材料,其构成定子和转子的铁磁材料的磁导率取决于磁场,我们将特别对此情况进行计算。
基本模型公式是磁场与矢量电势之间的关系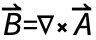 以及安培定律
以及安培定律 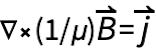 。
将它们组合在一起,并使用库仑计
。
将它们组合在一起,并使用库仑计 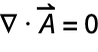 ,
,

假设电流仅在 z 方向上具有分量,为了简化问题,假设矢量电势的 x 和 y 分量为常数,并假设磁导率在 z 方向上也为常数。由此,在等式(10)中只有 z 分量是有效的,它是标量 u = Az 的 PDE:

对于磁导率 μ(B),使用根据以下测量数据拟合的方程。
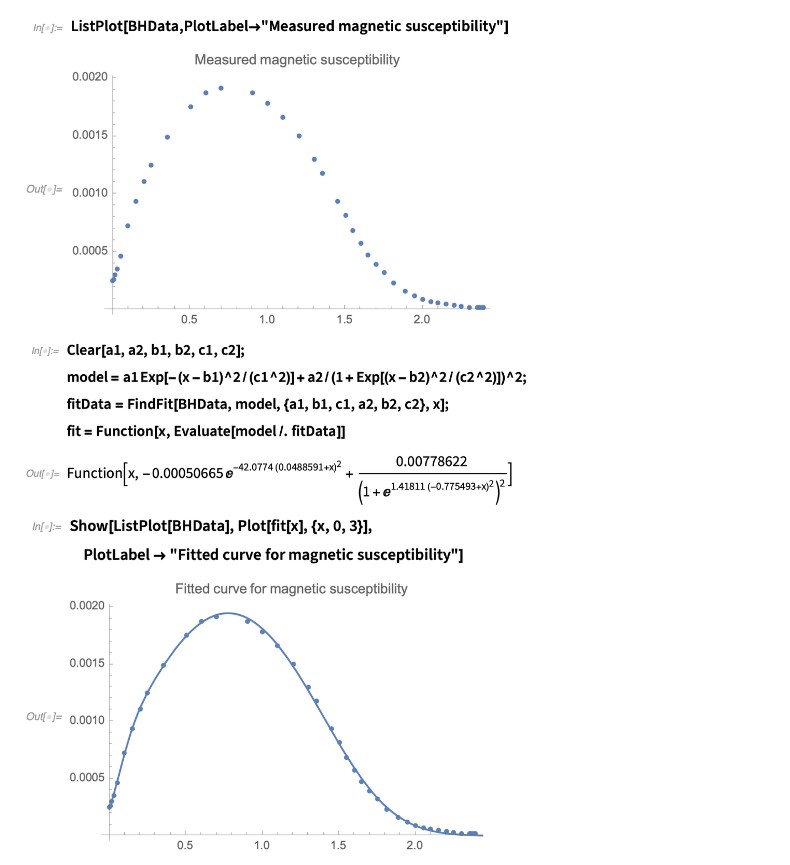
下图显示了电动机的横截面示意图,假设电流在黄色和橙色部分中沿垂直于屏幕的方向流动,则通过非线性 PDE 公式(11)计算磁场的强度分布。让我们计算一下。

设定磁导率并指定电流元件规格。在 NDSolve 中施加狄里克雷边界条件,即电动机定子外部的磁场为零。

将获得的结果与电机结构线框一起显示:
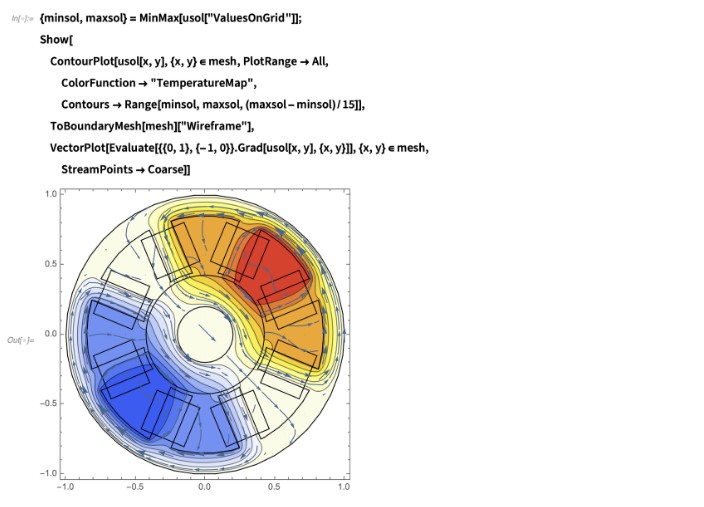
以下是描述稳态下不可压缩流体的 Navier-Stokes 方程:

上面第一个方程第二项中的对流项(在此,ρ = 1 且外力场为零)基本上是非线性的。此处,由于 u 是向量,如果是二维,则第一个方程式由两个方程式 ux 和 uy 组成,微分算子∇作用于该方程式(请参见下面的代码)。让我们计算二维空腔中的速度场。狄里克雷条件是填充在空腔中的流体的上侧以恒定速度 ux 驱动到右侧,剩余侧的通量为零,并且图形左下角的压力为零。Wolfram 语言代码如下:

可视化获得的速度场:

压力分布如下:
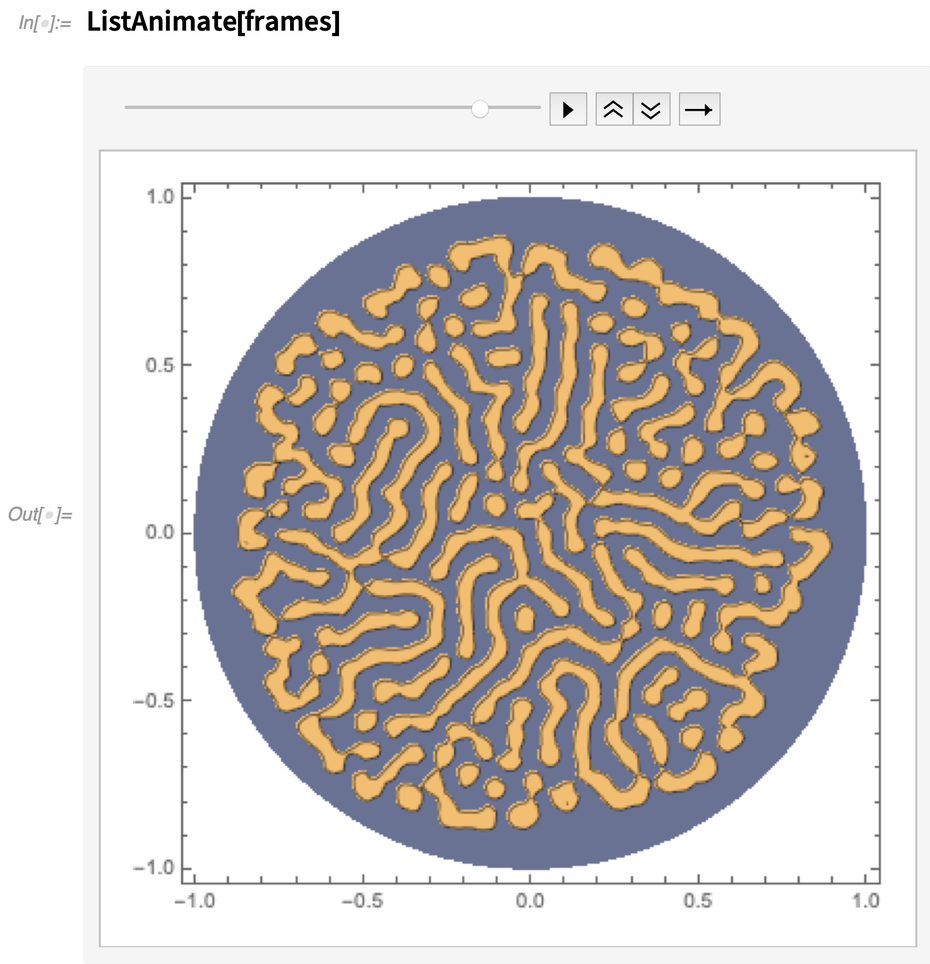
由于化学反应和物质扩散而导致的多种物质的浓度变化被称为反应扩散系统。以下以此为模型计算非线性联立 PDE(Gray-Scott 模型)的示例。从外部将作为原料的化学物质 U 连续地引入填充有另一种物质 V 的反应容器中,并进行自催化反应。

之后,U 变成最终产品 P,然后将 P 排放到系统外部。U 和 V 浓度 u 和 v 随时间变化所描述的就是这个模型:

Du 和 Dv 是各自的扩散系数,F 是物质 U 的补充率,K 是定义反应速度 V→P 的参数。从输入表达式到可视化(动画)的代码如下所示:

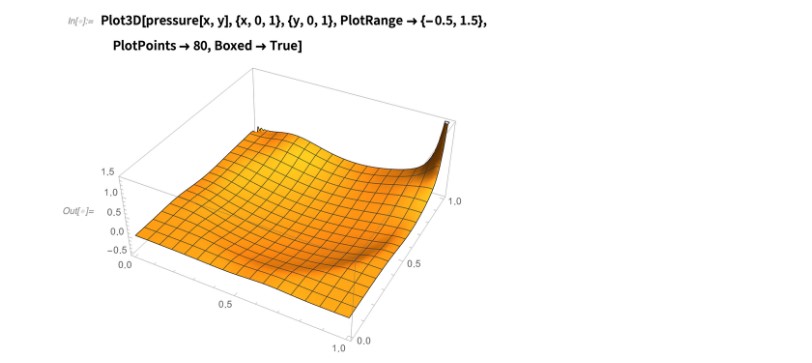
通过将随时间变化的项添加到公式(12),来描述随时间变化的不可压缩流体流动。
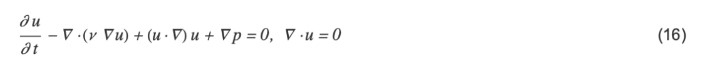
对于流体在两个无限宽的平行板间流动的状态,让我们计算一个无限长的圆柱体垂直于流向位于该空间中时的流速分布。未知数是速度(u,v)和压力 p,其中垂直于板和圆柱的平面为 xy 平面。Wolfram 语言代码如下。
Navier-Stokes 方程式:

设置入口处水池的大小和速度分布。定义 rampFunction,该函数可提供平滑的速度变化,以使速度在特定时间不会从零变为非零。由于流域的大小和流体速度,此处的雷诺数约为 200。

边界条件和初始条件:

速度分布从 t = 0 到 10 的变化是由 NDSolve 在监视 t 的同时计算的。在普通 PC (3.1GHz Intel Core i5,内存16GB) 上大约需要运算 6 分钟。

根据每个点的速度绝对值进行着色并创建动画。

可以确认以下为该区域生成的网格:

Mathematica 12(Wolfram语言 12)极大地扩展了有限元方法的应用范围,使得包括 Navier-Stokes 方程在内的许多非线性偏微分方程的求解变为可能。由于 Wolfram 语言在符号计算方面的优势,无论 PDE 形式如何,都可以在保证求解的高效性和统一性的同时,保证其高度通用性。有关 FEM 的内部处理的详细信息已经发布。与此同时,Mathematica 教程也对弹性分析、声学分析和热/振动传导分析等在许多领域的应用实例有详细说明,以供大家参考。
有限元编程:
网格生成和三角剖分:
ASAP/APEX技术交流群 373021576
SYNOPSYS光学设计与优化交流群 965722997
RP激光软件交流群 302099202
武汉墨光科技有限公司
友情链接
Copyright © 2012-2021 武汉墨光科技有限公司版权所有
许可证:鄂ICP备17024342号-1

