Wolfram 语言 & Mathematica 12.2 半年内上线了 228个新函数！

扩展了Mathematica和Wolfram语言在生物分子序列操作、PDE建模、空间统计和远程批处理作业计算中的功能，以及新的笔记本界面功能等：

·维图的绘制
·可以随便画的“画布”
·对 TeX 的全面支持
·等了36年的3D阵列图
·导入分析 PDF 文档
·生成视频并部署到云端
·拥有41种新日历 —— 包含中国的阴历
·八种新的地图样式
·可计算的“欧几里得”
·凸优化
·机器学习、神经网络与区块链
·添加对Arduino，Adafruit和SparkFun 等32余种微控制器的支持
·更加美炫美焕的可视化功能
·更多（https://www.wolfram.com/mathematica/quick-revision-history.html）

当我们在今年3月发布版本12.1时，我很高兴地说，它的182个新函数是我们有史以来最大的.1版本。但是仅仅九个月后，我们发布了更大的.1版本！今天发布的12.2版具有228个全新函数！

我们总是有一个正在进行中的开发项目系列，任何给定的项目都需要几个月甚至十几年才能完成。当然，这是对我们整个Wolfram语言技术栈的致敬，我们能够如此迅速地进行如此多的开发。但是版本12.2可能更令人印象深刻，因为我们直到今年6月中旬才专注于其最终开发。因为在3月到6月之间，我们专注于12.1.1版，那是一个“抛光版”。没有新功能，但修复了1000多个未解决的错误（最早的错误是1993年的文档错误）：

我们如何设计现在12.2中的所有这些新函数和新功能呢？有很多工作！我个人在上面也花费了很多时间（还有其他“小项目”，例如物理等）。但是在过去几年中，我们以非常开放的方式进行了语言设计——直播内部设计讨论，并实时获得各种出色的反馈。到目前为止，我们已经录制了大约550小时，其中版本12.2至少占用了150小时。

顺便说一下，除了12.2中的所有完全集成的新功能之外，Wolfram Function Repository中也有大量活动——甚至自从12.1发布以来，在那里已经添加了534种新的，用于各种特殊目的策选函数。

生物分子序列：符号 DNA、蛋白质等

在版本12.2的众多领域中，有太多不同的事物，很难知道从哪里开始。那让我们谈论一个全新的领域：生物序列计算。是的，我们在Wolfram语言中拥有基因和蛋白质数据已有十多年了。但是12.2中的新功能是利用生物序列进行灵活，通用计算的能力的开端。并以某种方式与我们在过去几年中一直在Wolfram 语言中添加的所有化学计算能力相适应。

这是我们表示DNA序列的方式（是的，这也适用于很长的序列）：

我必须说，我对将“我们的”生物学细节放入我们的核心语言中的“非普遍性”感到有些苦恼……但最终还是动摇了我的想法，当然，我们所有的用户（目前）都是确定的真核生物。毋庸置疑，我们也可以处理生活中的其他分支：

还有一些新功能，例如BioSequenceInstances，用于解决退化字符：

空间统计与建模

燕窝、金矿、待售房屋、材料缺陷、星系的位置等。这些都是空间点数据集的示例。在版本12.2中，我们现在拥有处理这些数据集的广泛函数。

这是美国各州首府所在地的“空间点数据” ：

假设您在州首府，这是在一定距离之外找到最近的其他州首府的可能性：

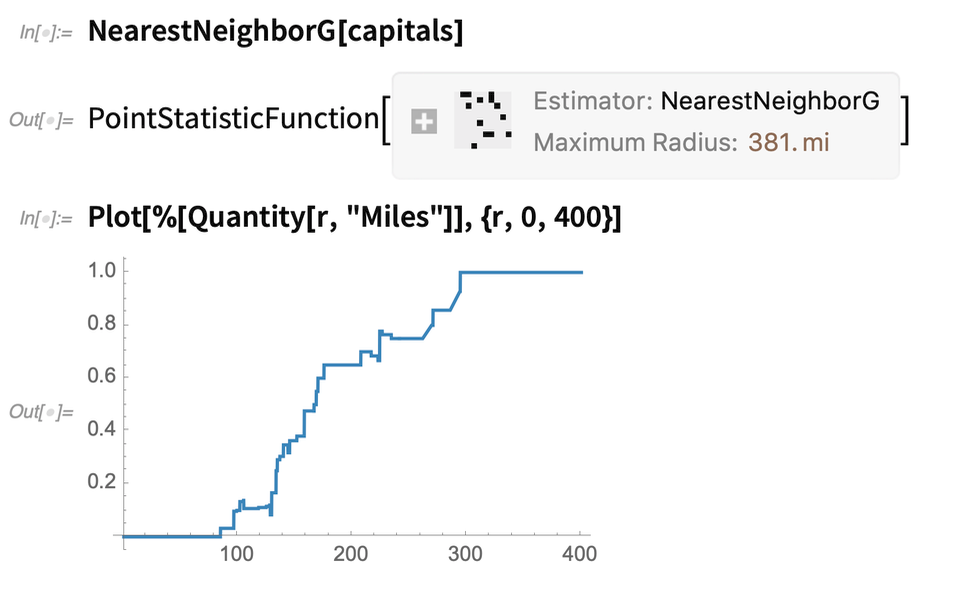
然后测试州政府是否是随机分布; 不用说，它们不是：

SpatialRandomnessTest [capitals]
0.

除了根据空间数据计算统计信息外，版本12.2还可以根据各种模型生成空间数据。这是一个模型，该模型随机选择“中心点”，然后在它们周围聚集其他点：

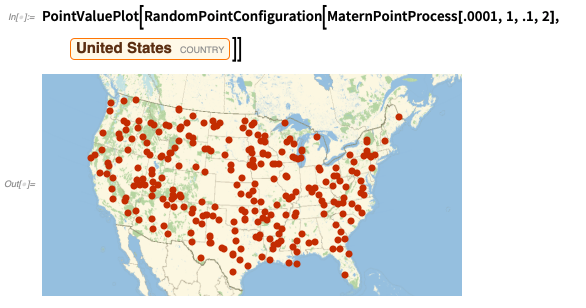
您也可以采用另一种方法，使空间模型拟合数据：

1、 EstimatedPointProcess[capitals,
2、MaternPointProcess[\[Mu], \[Lambda], r, 2], {\[Mu], \[Lambda], r}]

便捷的实际 PDE

在某些方面，我们已经为此努力了30年。我们首先在版本 2.0 中引入了NDSolve，从那时起我们一直在稳步增强它。但是，我们的长期目标一直是方便处理在高端工程中经常出现的实际 PDE。在版本 12.2中，我们最终获得了所有基础算法技术，可以创建真正精简的 PDE 求解体验。

那么您如何指定 PDE？过去，它总是根据特定的导数、边界条件等来明确进行的。但是，例如，在工程中使用的大多数 PDE 都由高级分量组成，将导数、边界条件等“打包在一起”以表示物理，材料等的特征。

我们新的 PDE 框架的最低层由符号“项”组成，这些“项”对应于实际PDE中出现的常见数学构造。例如，这是一个二维“拉普拉斯项”：

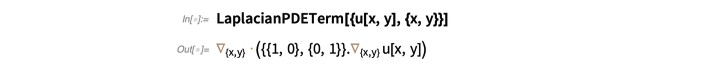
现在，这就是查找正则多边形中拉普拉斯算子的前5个特征值的全部步骤：

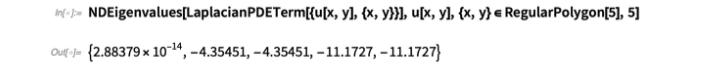
重要的是您可以将这种操作放入整个管道中。像这里一样，我们从图像中获取区域，求解第十个本征模，然后3D绘制结果：

除了 LaplacianPDETerm 之外，还有 DiffusionPDETerm 和ConvectionPDETerm 之类的东西，它们代表了实际 PDE中出现的其他项。这是具有单位扩散系数的各向同性扩散的项：

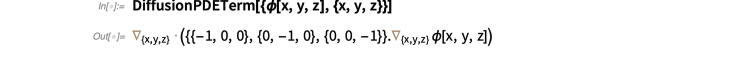
除了单个项外，还有一些“分量”将多个项（通常带有各种参数）组合在一起。这是Helmholtz PDE分量：

顺便说一句，值得指出的是，我们的“项 (term) ”和“分量 (components)”被设置为代表PDE的符号结构，其形式适用于结构操纵和数值分析之类的事物。为了确保它们保持其结构，它们通常以灭活形式 (inactive) 保存。但是，如果要执行代数运算之类的操作，则始终可以“激活”它们：

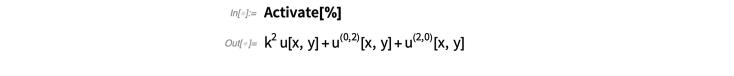
在实际的 PDE中，人们经常要处理发生在实际物理材料中的实际物理过程。在版本12.2中，我们有了直接的方法，不仅可以处理扩散问题，还可以处理声学、传热和传质——并提供实际材料的特性。通常，结构是有一个PDE“分量”代表材料的整体行为，还有各种PDE“值”或“条件”代表边界条件。

这是一个典型的PDE分量，使用Wolfram知识库中的材料属性：

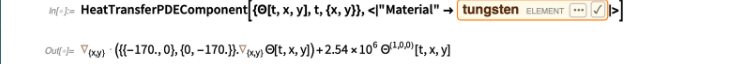
可能的边界条件有很多多样性和复杂性。例如，对于热传递，有HeatFluxValue，HeatInsulationValue和其他五个符号边界条件规范构造。在每种情况下，基本思想都是说条件在何处（几何上）适用，然后适用于什么，以及与之相关的参数。

因此，例如，这里有一个条件，即指定有一个固定的“表面温度” θ ₀，在由 X²+Y²=1定义的（圆）区域的外面：

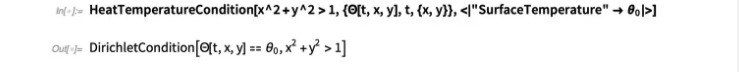
这里基本上发生的是，我们的高级“物理”描述被“编译”为显式的“数学” PDE结构，例如 Dirichlet 边界条件。

好吧，那么这一切在现实生活中如何融合在一起？让我举一个例子。但首先，让我讲一个故事。早在2009年，我就和我们的主要PDE开发人员一起喝茶。我拿起一茶匙问：“我们什么时候可以模拟其中的压力？” 我们的首席开发人员解释说，要达到这一点还需要做很多工作。现在，我很高兴地说，经过11年的努力，在版本12.2中，我们实现了！为了证明这一点，我们的首席开发人员刚刚给了我……（可计算的）勺！

计算的核心是3D扩散PDE项，其“扩散系数”由杨氏模量（此处为Y）和泊松比（ν）参数化的4阶张量给出：

PDE建模是一个复杂的领域，我认为这是一项重大成就，我们现在设法将其打包成“干净”的包装。但是在版本12.2中，除了PDE建模的实际技术外，其他重要的是有关PDE建模的大量计算论文——总共约400页的详细解释和应用示例，当前涉及声学、传热和传质，但还有许多其他领域。

只需输入 T _E X

Wolfram语言就是用精确的计算语言表达自己。但是在笔记本中，您也可以用自然语言的普通文本表达自己。但是，如果您也想在那里显示数学怎么办？25 年来，我们就完成了基础设施做数学显示——通过我们的盒子语言。但是，进入数学的唯一便捷方法是通过Wolfram语言数学架构——从某种意义上说，它们必须具有计算意义。

但是，“仅用于人眼”的“数学”呢？您具有要指定的某种视觉布局，但是不一定具有已定义的任何特定基础计算含义吗？好了，几十年来，一直有一种指定此类数学的好方法，这要感谢我的朋友Don Knuth：只需使用TEX 即可。在版本12.2中，我们现在支持将 TEX 数学直接输入到台式机和云中的Wolfram笔记本中。在下面，TEX 正在变成我们的盒子代表，所以它结构上与一切可以互操作。但是您可以将其输入并编辑为TEX 。

该界面与Wolfram | Alpha风格自然语言输入的Ctrl+=界面非常相似。但是对于T _E X（向标准T _E X分隔符致敬），它是Ctrl + $。

键入Ctrl + $，您会得到一个T _E X输入框。完成T E _EX后，只需按RET，它将被渲染：

像Ctrl +=，如果单击呈现形式，它会回到文本，您可以重新编辑，就像T E X。

在文本单元格中输入T _E X是最常见的事情。但是版本12.2还支持在输入单元格中输入T _E X：

如果你运行一下会怎样？您的输入将被视为TraditionalForm，并且至少会尝试对其进行解释。当然，如果您编写了“无意义的计算数学”，那将是行不通的。

随便画

输入Canvas []，您将得到一个空白的画布以绘制所需的内容：

我们一直在努力使绘图工具尽可能符合人体工程学。

应用Normal会为您提供图形，然后您可以使用或操纵它们：

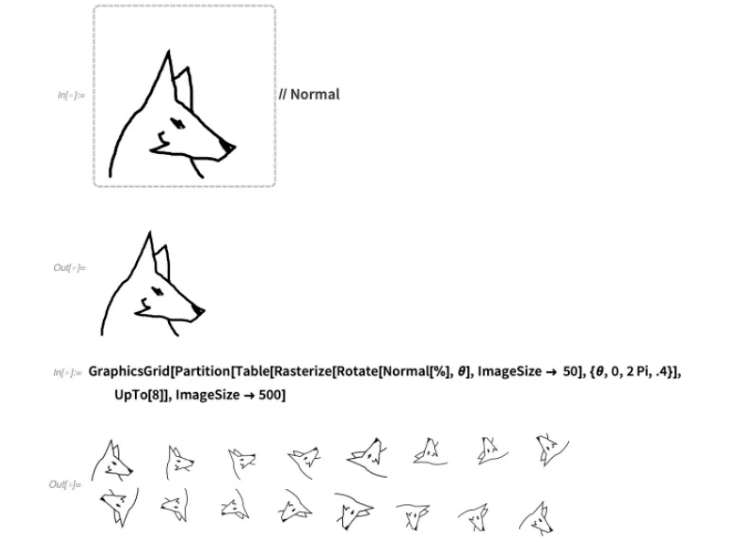
创建画布时，它可以具有任何图形作为初始内容，并且可以具有所需的任何背景：