Confirm/Enclose：符号异常处理

你的程序内部曾经出现过问题吗？如果是这样，该程序应该怎么做？如果人们忽略这样的事情，就有可能写出非常优雅的代码。但是，一旦人们开始进行检查，查找问题发生的逻辑，代码就会变得更加复杂，并且可读性大大降低。

一个人能做些什么？好吧，在版本12.2中，我们开发了一种高级符号机制来处理代码中出错的地方。基本上，您的想法是插入“Confirm”（或相关函数），就像您可能插入Echo一样，以“确认”程序正在执行应做的事情。如果确认有效，则您的程序将继续进行。但是，如果失败，程序将停止并退出到最近的封闭式 Enclose。从某种意义上说，Enclose“封闭”程序区域，而不是让内部出错的任何内容立即传播出去。

让我们看看这在一个简单的情况下如何工作。在这里，Confirm成功地“确认”了y，只返回了它，而Enclosure并没有做任何事情：

Enclose[f[x, Confirm[y], z]]
f[x,y,z]

但是现在让我们用$Failed代替y。$Failed是默认情况下Confirm 认为有问题的。因此，当它看到$Failed 时，它将停止，退出到Enclose，这又产生一个Failure对象：

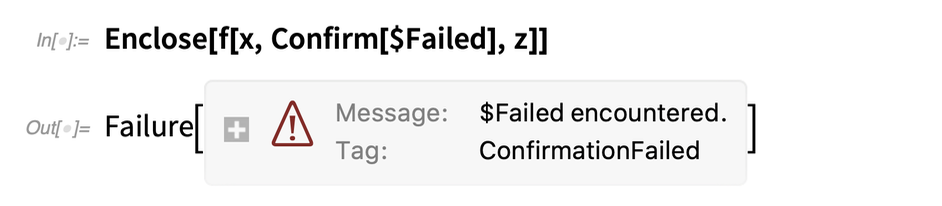
如果放入Echo，我们将看到 x 已成功达到，但 z 没有达到；一旦 Confirm 失败，则停止一切：

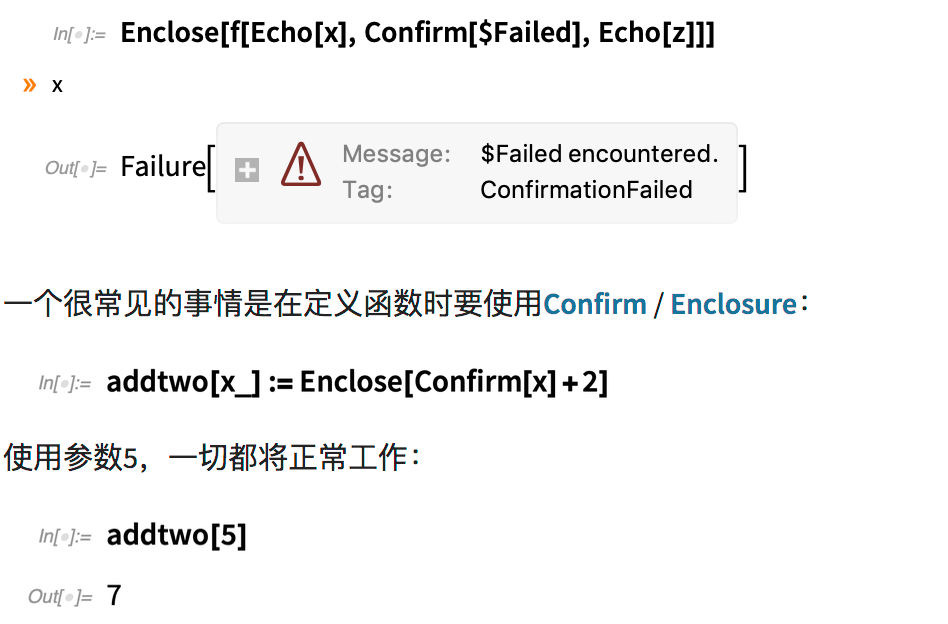
但是，如果我们改用Missing []（默认情况下Confirm认为是有问题的），则会返回Failure对象：

我们可以使用If，Return等等来实现相同的目的。但是即使在这种非常简单的情况下，它看起来也不是很好。

Confirm具有某些默认的东西，它认为是“错误”（示例为$ Failed， Failure [...]或Missing [...]）。但是有一些相关函数可以让您指定特定的测试。例如， ConfirmBy 可作用于函数来测试是否应确认表达式。

在这里，ConfirmBy 确认2是一个数字：

Enclose[f[1, ConfirmBy[2, NumberQ], 3]]
f[1,2,3]

但是NumberQ并不这样认为 x：

但是，这里才是很多美好事情的开始。假设我们将 world 映射到列表上，并始终确认它会获得良好的结果。这里一切正常：

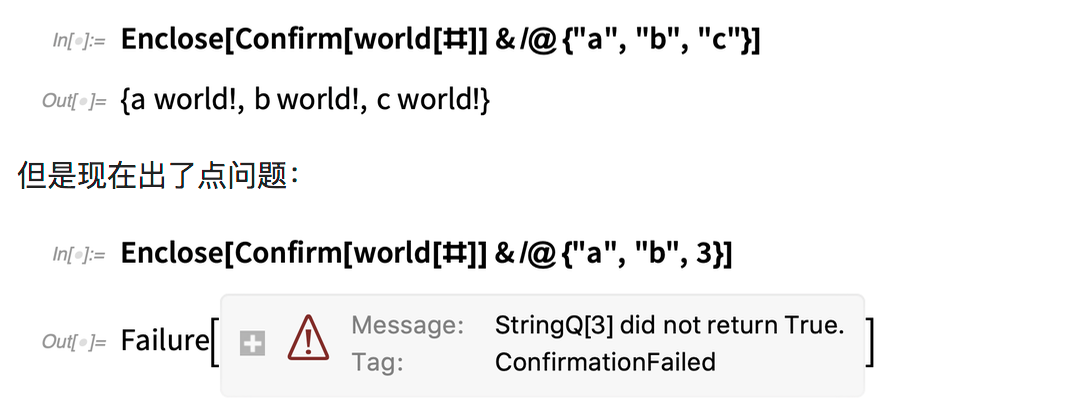
在 world 定义中的 ConfirmBy 失败，导致它包含的 Enclose 产生Failure的对象。然后，此 Failure 对象导致 Map 内的 Confirm 失败，并且包含的Enclosure给出了整个对象的Failure对象。再一次，我们可以使用If，Throw，Catch等实现相同的功能。但是Confirm / Enclosure可以更鲁棒，更优雅地完成它。

这些都是非常小的例子。但是，Confirm / Enclose真正显示其价值的地方在于大型程序，以及提供清晰，高级的框架来处理错误和异常以及定义其范围。

除了Confirm和ConfirmBy之外，还有ConfirmMatch，它确认表达式匹配指定的模式。然后是ConfirmQuiet，它确认表达式的求值不会生成任何消息（或者至少不告诉您要对其进行测试的任何消息）。还有ConfirmAssert，它只需要一个“断言”（例如p> 0）并确认它是正确的。

当确认失败时，程序将始终退出到最近的 Enclose，将包含有关已发生故障的信息的Failure对象传递到Enclose。当您设置了Enclose，你可以告诉它如何处理收到的失败对象，要么只是返回他们（也许包含 Confirm 和 Enclose 的），或对内容应用函数。

Confirm和Enclose是用于处理错误的强有力机制，可以轻松简单地将其插入程序。但是，不用说，它们肯定有一些棘手的问题。让我只举一个例子：问题是：给定的 Enclose 真正封装的是哪个 Confirm？如果您编写的一段代码明确包含Enclose和Confirm，那么这很明显。但是，如果在某个函数栈内部深入生成了一个Confirm（也许是动态生成），该怎么办？这类似于命名变量的情况。Module 只是在其体内直接（“按词法”）查找变量。Block在任何可能出现的地方寻找变量（“动态地”）。好吧，默认情况下，Enclose 的工作方式类似于Module，“按词法”查找要封装的Confirm。但是，如果在Confirm和Enclosure中包含标签，则即使它们在同一段代码中未明确“可见”，也可以将它们设置为“互相查找”。

函数强化

Confirm/Enclose提供了一种很好的高级方法来处理程序或函数内部发生问题的“流程”。但是，如果一开始有什么不对的地方怎么办？在我们的内置Wolfram语言函数中，我们应用了一组标准的检查。参数是否正确？如果有选项，是否允许它们使用，并且位置是否正确？在版本12.2中，我们添加了两个功能，可以对您编写的函数执行这些标准检查。

这表示 f 应该有两个参数，在这里它却有三个参数：

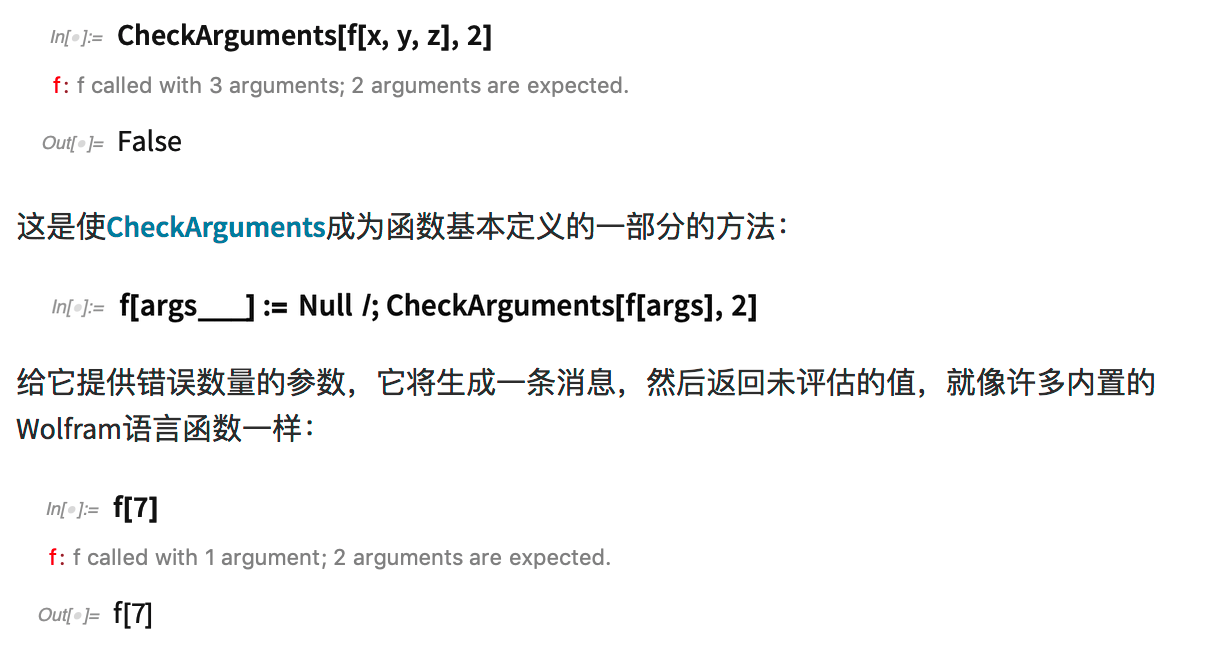
ArgumentsOptions 是版本12.2中的另一个新函数——将“位置参数”与函数中的选项分开。设置函数的选项：

Options[f] = {opt -> Automatic};

这需要一个位置参数，它会发现：

ArgumentsOptions[f[x, opt -> 7], 1]
{{x},{ opt->7}}

如果找不到确切的一个位置参数，则会生成一条消息：

代码清除

您运行一段代码，它就会执行它的工作——通常，您不希望它留下任何东西。通常，您可以使用诸如Module、Block、BlockRandom等的作用域构造来实现此目的。但是有时候，您设置的某些内容需要在代码完成后明确“清理”。

例如，您可能在代码段中创建了一个文件，并希望在该代码段完成时删除该文件。在版本12.2中，有一个方便的新函数可用于管理此类内容：WithCleanup。

WithCleanup[expr，cleanup]评估expr，然后进行清理——但从expr返回结果。这是一个简单的示例（使用Block可以更好地实现）。您正在为x分配一个值，获取其平方，然后在返回平方之前清除 x：

WithCleanup[x = 7; x^2, Clear[x]]
49

仅具有一个在执行清理操作的同时仍返回您正在评估的主表达式的结构已经很方便了。但是WithCleanup的一个重要细节是，它还可以处理您中止正在执行的主要评估的情况。通常，发出异常终止将导致一切停止。但是WithCleanup的设置是为了确保即使中止也可以进行清理。因此，例如，如果清理涉及删除文件，则即使主操作被终止，该文件也会被删除。

WithCleanup还允许进行初始化。因此，初始化和清理一样在这里完成，但是主要计算被中止：

顺便说一句，WithCleanup也可以用来Confirm/Enclose，以确保即使确认失败，一定会清理完成。

日期——带有37个新日历

今天是2020年12月16日，至少要按照美国通常使用的标准公历来定。但是世界上还有许多其他用途的日历系统正在使用，甚至历史上曾经被一次或多次使用。

在Wolfram语言的早期版本中，我们支持一些常见的日历系统。但是在版本12.2中，我们添加了对日历系统的非常广泛的支持——共有41种。可以认为日历系统有点像大地测量学中的投影或几何中的坐标系。您有某种时间日期：现在您必须知道它在所使用的任何系统中如何表示。与GeoProjectionData一样，现在有CalendarData可以为您提供可用日历系统的列表：

CalendarData["DateCalendar"]
{"AbsoluteTime", "ArithmeticFrench", "ArithmeticPersian", \
"AstronomicalFrench", "AstronomicalPersian", "AztecTonalpohualli", \
"AztecXihuitl", "Babylonian", "BalinesePawukon", "Chinese", "Coptic", \
"Ethiopic", "Gregorian", "HankeHenryPermanent", "Holocene", \
"InternationalFixed", "Icelandic", "Islamic", "ISOWeek", \
"ISOOrdinal", "Japanese", "Jewish", "Julian", "JulianDate", \
"MayanHaab", "MayanLongCount", "MayanTzolkin", "ModernHinduSolar", \
"ModernHinduLunisolar", "Newtonian", "ObservationalHebrew", \
"ObservationalIslamic", "OldHinduLunisolar", "OldHinduSolar", \
"RataDie", "Samaritan", "Symmetry454", "Tibetan", "UnixTime", \
"WesternBahai", "World"}

因此，以下是“Now”转换为不同日历的表示形式：

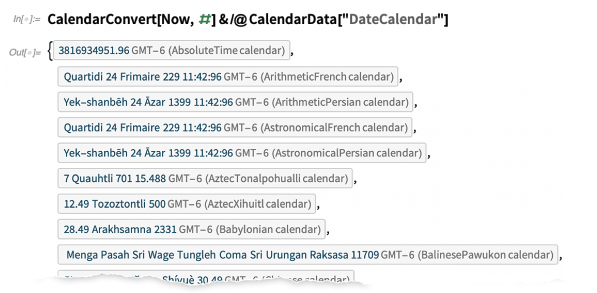
这里有很多微妙之处。有些日历纯粹是“算术”的；其他则依靠天文计算。然后是“闰变量”问题。对于公历，我们习惯于仅添加2月29日。但是，例如，中国日历可以在一年之内添加整个“闰月”（例如，可以有两个“四月”）。在Wolfram 语言中，我们现在可以使用 LeapVariant 来表示此类事情：

地理新函数

到目前为止，Wolfram语言在地理计算和地理可视化方面具有强大的功能。但是我们正在继续扩展地理功能。在版本12.2中，一个重要的附加功能是空间统计信息（如上所述），它与地理完全集成。但是，还有一些新的地理图元。一个是GeoBoundary，它计算事物的边界：

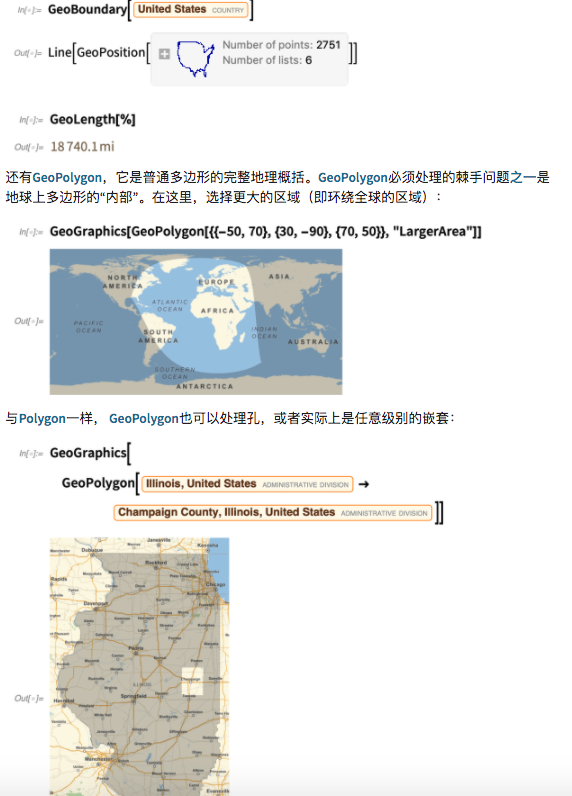
但是，地理学最大的“吸引力”是x。在版本12.2中，它仍是初步的（尚未完成），但是至少对基于矢量的地图渲染具有实验性的支持。最明显的收获是，在所有比例尺下，地图看起来都更加清晰明了。但是另一个好处是我们可以为地图引入新的样式，并且在版本12.2中，我们包括了八种新的地图样式。

这是我们的“旧式”地图：

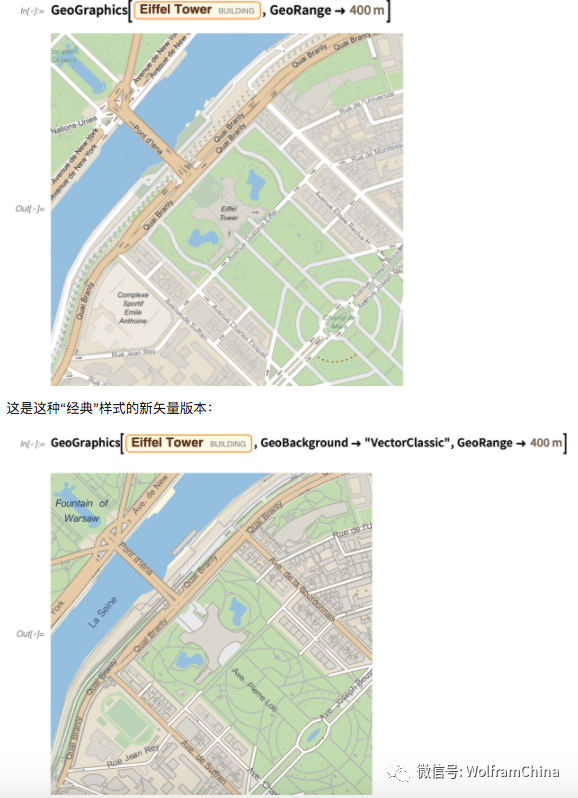
这是一种新的（矢量）样式，适用于网络：

导入PDF

是否要分析PDF文档？十多年来，我们已经能够从PDF文件中提取基本内容。但是PDF是一种高度复杂（并且不断发展）的格式，许多“野生”文档都具有复杂的结构。但是，在版本12.2中，我们极大地扩展了PDF导入功能，例如，从arXiv 提取随机论文并导入使它变得现实起来：

这将从纸张中挑选出所有图像，并对其进行拼贴：

根据它们的产生方式，PDF可以具有各种结构。“ContentsGraph”给出了一个图表，该图表表示为文档检测到的整体结构：

最新的工业强度凸优化

从版本12.0开始，我们一直在添加用于解决大规模优化问题的最新功能。在版本12.2中，我们继续完善这些功能。

一项新功能是超级函数 ConvexOptimization，它可以自动处理线性、线性分数、二次、半定和圆锥形优化的全部范围，同时提供最优解及其双重属性。在12.1中，我们增加了对整数变量的支持（即组合优化）。在12.2中，我们还添加了对复杂变量的支持。

但是12.2中最大的优化新事物是引入了鲁棒优化和参数优化。鲁棒优化使您可以找到在某些变量的整个值范围内有效的最优值。参数优化可让您获得一个参数函数，该函数为特定参数的任何可能值提供最佳选择。因此，例如，对于任何（正）α 值，这找到 x，y 的最佳值：

与Wolfram语言中的所有内容一样，我们付出了很多努力来确保凸优化功能无缝集成到系统的其余部分中，因此您可以象征性地设置模型，并将其结果传递到其他函数中。我们还包括了一些非常强大的凸优化求解器。但是特别是如果您正在执行混合（即实数+整数）优化，或者您正在处理非常大的问题（例如一千万个变量），我们还可以访问其他外部求解器。因此，例如，您可以使用Wolfram语言作为“代数建模语言”来设置问题，然后（假设您具有适当的外部许可）只需将“方法”设置为“Gurobi”或“Mosek”您可以使用外部求解器立即解决问题。（而且，顺便说一下，我们现在有了一个开放的框架，可以添加更多求解器。）

支持组合器和其他正式构建块

可以说，我们在Wolfram语言中非常依赖的整个符号表达（及其变换）的思想源于组合器，而组合器刚刚在2020年12月7日迎来了其百年华诞(https://writings.stephenwolfram.com/2020/12/combinators-a-centennial-view/)。与原始组合器相比，我们在Wolfram语言中拥有的符号表达形式在很多方面都更加先进和可用。但是在版本12.2中（部分是为庆祝组合器），我们希望为原始组合器添加一个框架。

因此，例如，现在我们有适当渲染的 CombinatorS，CombinatorK等：

CombinatorS[CombinatorK]
S[K]

但是，我们应该如何表示一个组合器对另一个组合器的应用？今天我们这么写：

f@g@h@x
f[g[h[x]]]

但是在数学逻辑的早期，有一个不同的约定——涉及左关联应用，其中一个期望的“组合样式”从将函数应用于事物而生成“函数”而不是“值”。因此，在12.2，我们推出了一个新的“应用操作符”Application，显示为.（输入为\[Application]或(Esc AP Esc)：

但是，人们也可以将组合器更“代数”地定义为表达式之间的关系，并且AxiomaticTheory 中现在有其专门的理论。

在12.2中，还向 AxiomaticTheory中添加了其他一些理论，以及一些新属性。

欧式几何互动

12.0版的主要进步之一是引入了用于欧几里得几何的符号表示形式：您可以指定符号GeometricScene，给出各种对象和约束，然后Wolfram语言可以“解决”它，并绘制一个随机图。满足约束的实例。在版本12.2中，我们进行了交互，因此您可以在图中移动点，并且所有内容（如果可能）都将以交互方式重新排列，以保持约束。

这是一个简单的几何场景的随机实例：

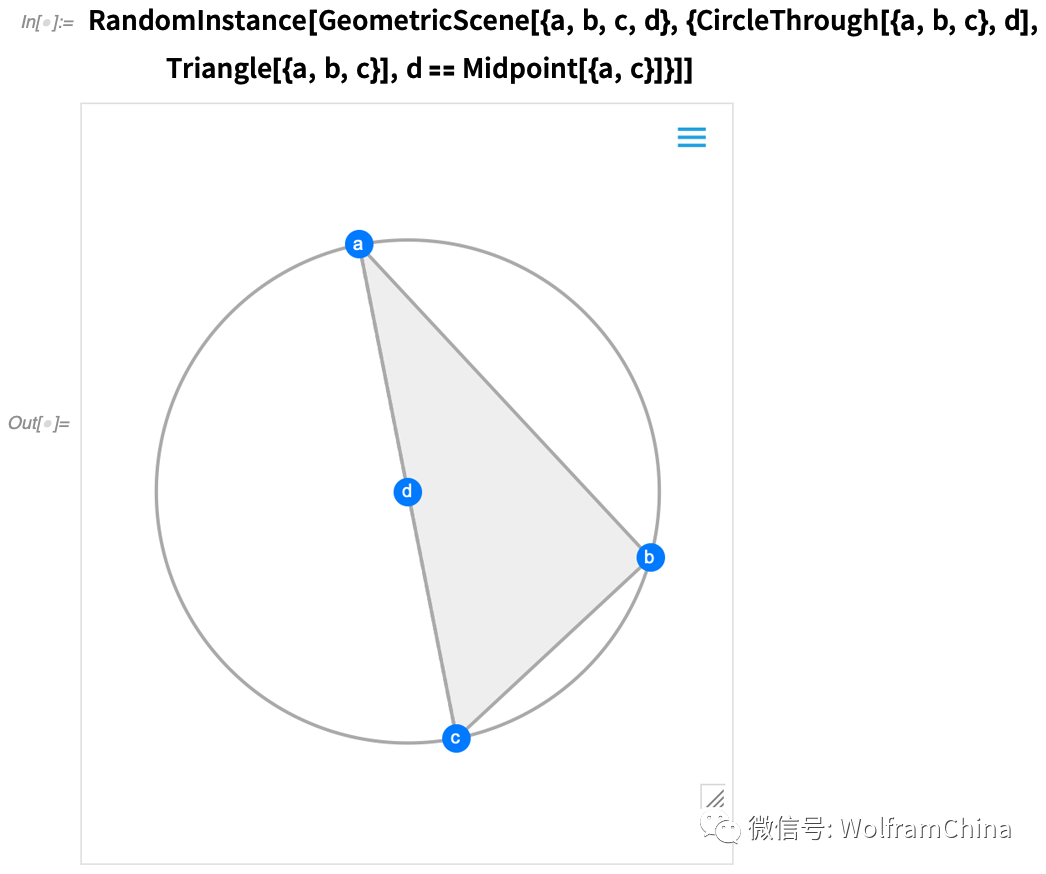
如果您移动一个点，则将交互式地重新排列其他点，以保持在几何场景的符号表示中定义的约束：

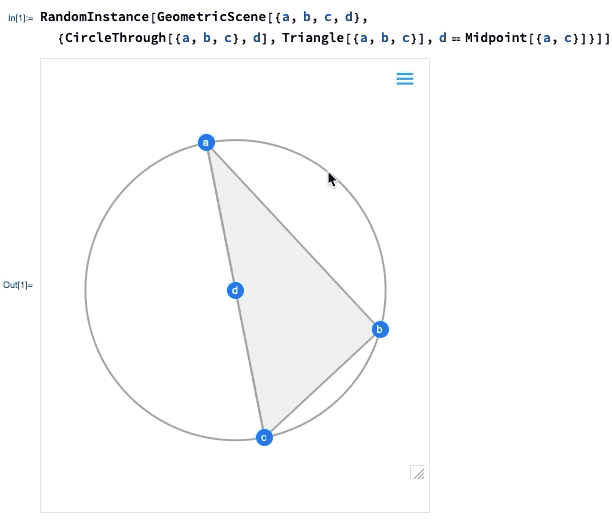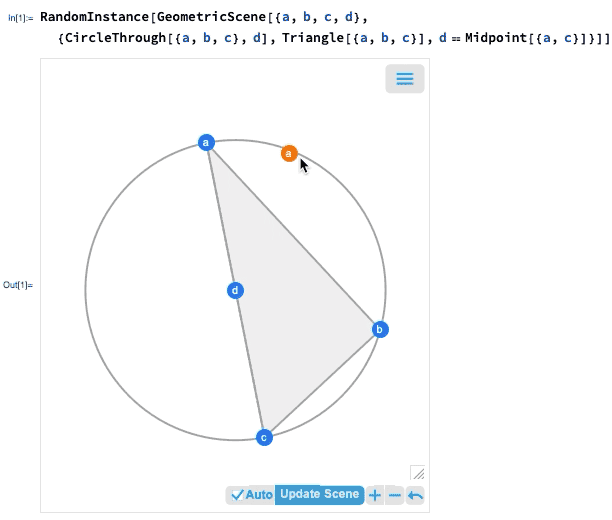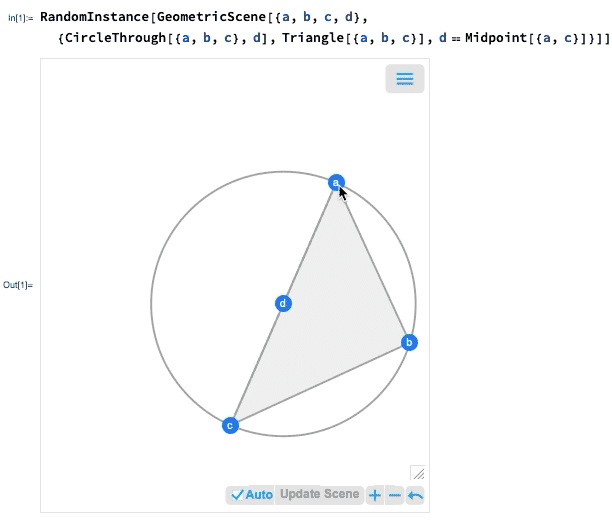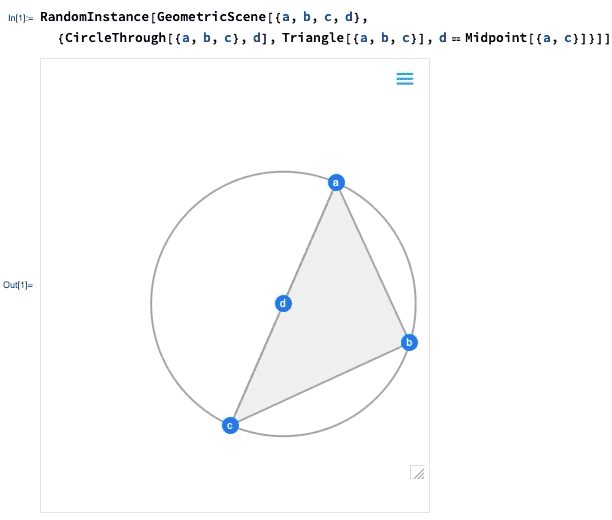
里面到底是怎么回事？基本上，几何已转换为代数。如果需要，可以得到代数公式：

您获得的第一个图像基本上是构建的结果。而且，像所有其他几何场景一样，它现在是交互式的。但是，如果将鼠标悬停在它上面，您将获得一些控件，可让您移至较早的步骤：

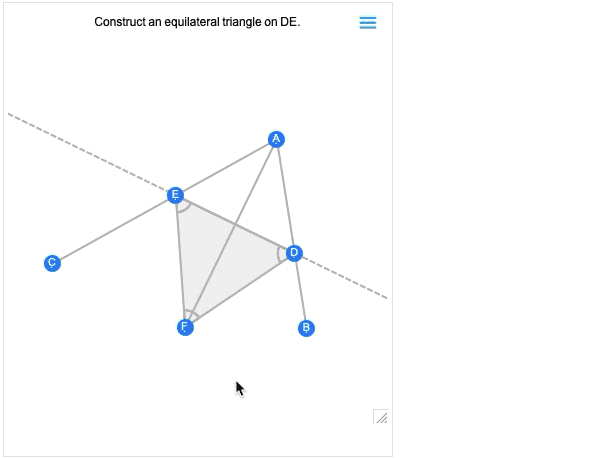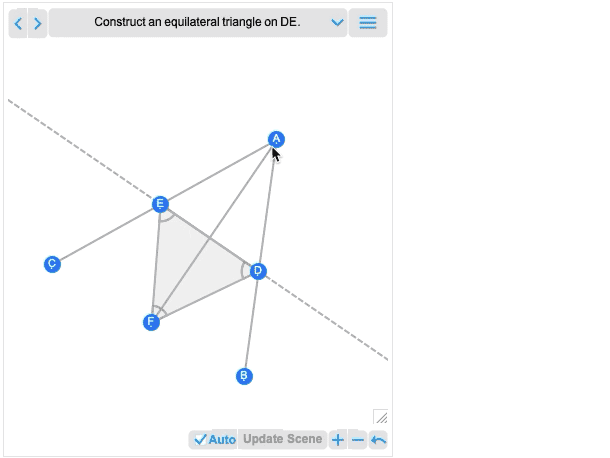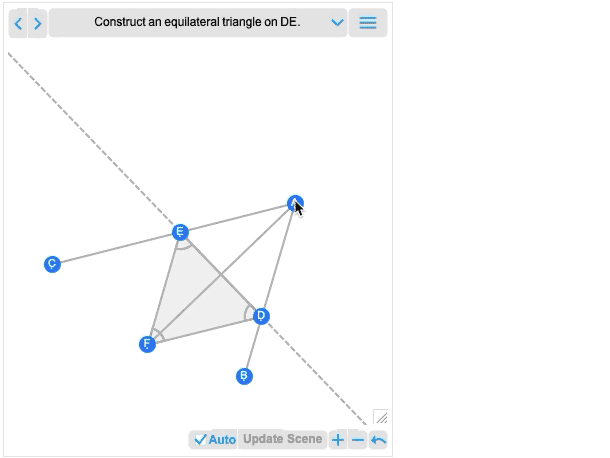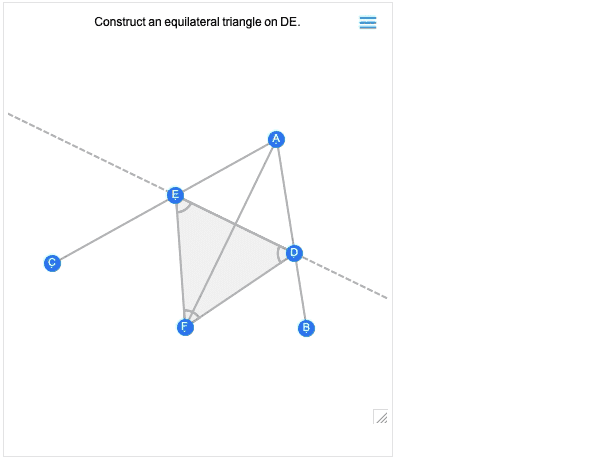
在较早的步骤上移动一个点，您将看到对以后的构建步骤有什么影响。

欧几里得的几何学是我们所知道的第一个数学公理系统。因此，在2000多年后，我们终于可以使它变得可计算是令人兴奋的。（是的，它最终将与AxiomaticTheory，FindEquationalProof 等联系起来。）

但是，考虑到Euclid最初的几何公式的重要性，我们添加了他的命题的可计算版本（以及其他“著名的几何定理”）。上面的示例是《Euclid’s book 1》中命题9。现在，例如，我们可以用希腊语获得他对此的原始陈述：

知识库中还有更多种类的知识

Wolfram语言作为一种全面的计算语言，其故事的重要组成部分是它对我们有关世界的庞大数据知识库的访问。自从版本12.1以来，知识库一直在不断地更新和扩展，实际上，从本质上讲，所有域都已更新了数据（通常是大量的数据），或者添加或修改了实体。

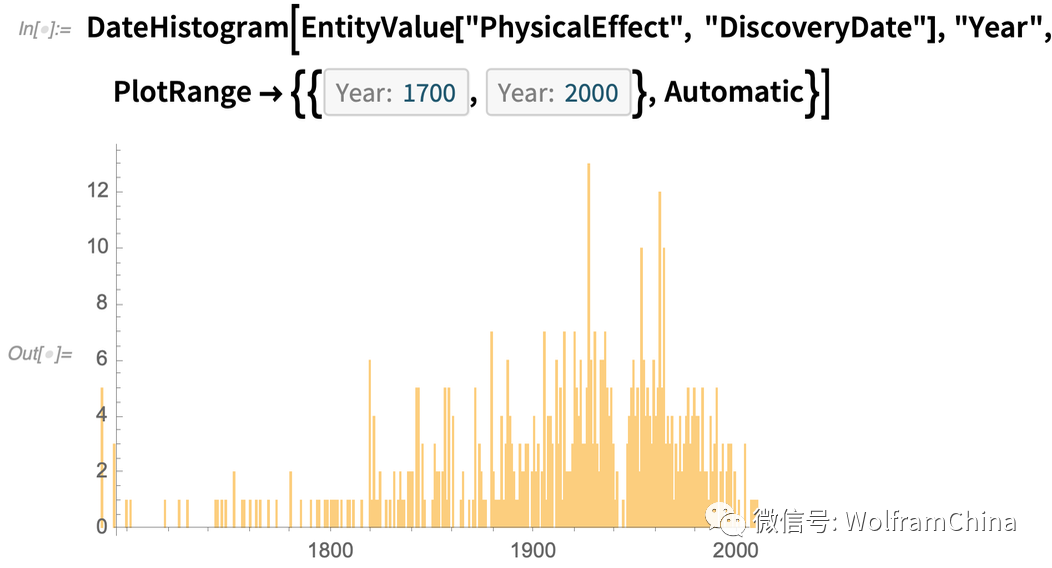
但是，作为已完成操作的示例，让我提及一些补充内容。食物是引起广泛关注的领域。到现在为止，我们已经掌握了超过一百万种食品的数据（相比之下，一家典型的大型杂货店可能存储着3万种食品）。随机选择食物：

作为可以使用该域中所有数据完成操作的示例，以下是发现这些影响的日期的直方图：

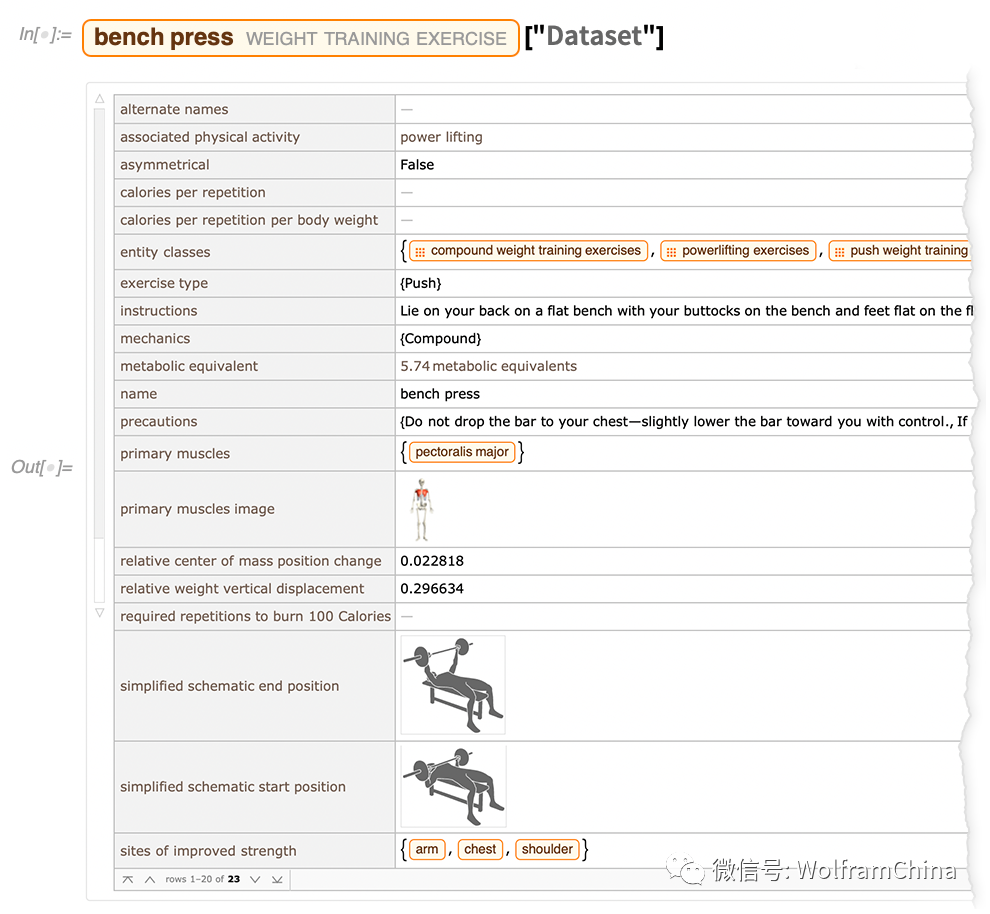
作为我们一直在努力的另一示例，现在还可以（嘲讽为）“举重”领域——举重锻炼：

Wolfram知识库的一个重要功能是它包含符号对象，它们不仅可以表示“普通数据”（如数字或字符串），还可以表示完整的计算内容。以此为例，版本12.2允许直接在知识库中访问Wolfram演示项目——及其所有有效的Wolfram语言代码和笔记本。以下是一些随机演示：

而且由于一切都是可计算的，因此可以立即制作一个特定主题的所有演示的图像拼贴：

机器学习的持续故事

自从我们首次引入Classify和Predict以来，已经过去了将近7年，并开始将神经网络完全集成到Wolfram语言中。有两个主要方向：第一个方向是开发“超函数”，例如Classify和Predict，它们尽可能自动地执行基于机器学习的操作。第二个方向是提供一个强大的符号框架，以利用神经网络的最新进展（尤其是通过Wolfram神经网络存储库），并允许灵活的持续开发和实验。

版本12.2在这两个方面都有进展。FaceRecognize是新的超函数的一个示例。给它一些标记过的面孔示例，它将尝试在图像、视频等中识别它们。让我们从网络搜索中获取一些训练数据（是的，有点乱）：

有很多新图标，但现在也有一个明确的约定，即圆圈代表固定的网络元素，而正方形代表可训练的元素。另外，如果图标中的边框较粗，则表示内部还有一个附加网络，您可以通过单击来查看。

无论是来自NetModel的网络，还是您自己构建的网络（或两者的组合），提取网络的“摘要图形”通常都很方便，例如，您可以将其放入文档或出版物中。Information 提供了几个摘要图形级别：

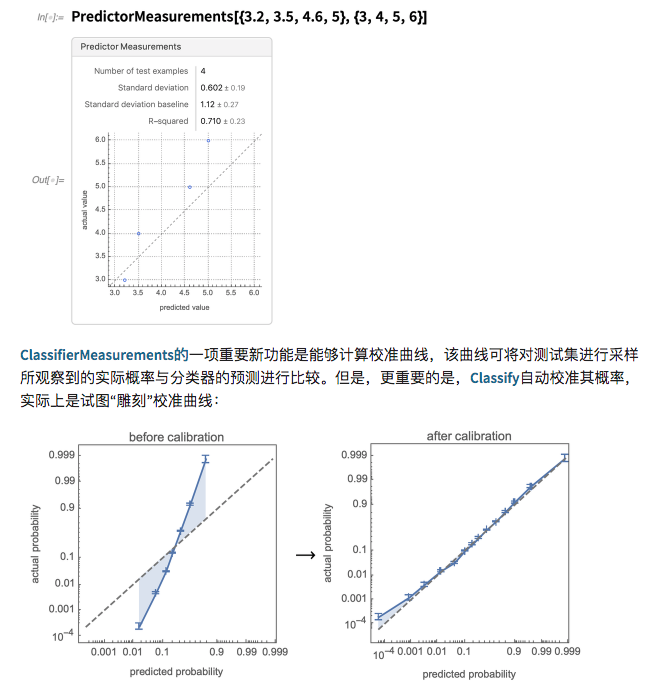
框架的另一项增强与模型诊断有关。多年前，我们引入了PredictorMeasurements 和 ClassifierMeasurements 以提供模型性能的符号表示。在版本12.2中（响应许多请求），我们可以提供最终的预测（而不是模型）来创建 PredictorMeasurements 对象，并且简化了 PredictorMeasurements 对象的外观和操作：

12.2版还开始了对神经网络构建方式的重大更新。一直以来，基本的设置是将一定的层集合放在一起，以暴露通过图形中的显性边缘连接的数组索引的数量。现在，版本12.2中引入了FunctionLayer，它使您可以更接近于普通的Wolfram语言代码。例如，这是一个特定的函数层：

这是此函数层作为显式NetGraph的表示形式：

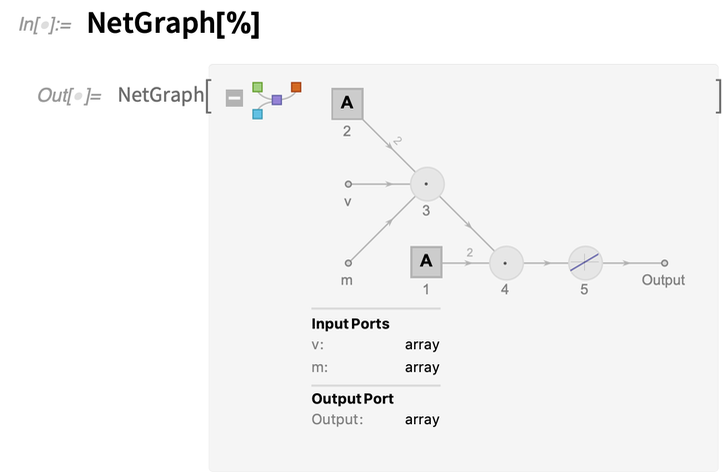
v和m称为“输入端口”。所述NetArray——由方形图标在网图形上标示，是一个可学习阵列，这里只包含两个元素。

在某些情况下，使用仅将层连接在一起的“基于块”（或“图形”）编程方法会更容易（而且我们一直在努力确保尽可能自动地进行连接）。但是在某些情况下，使用FunctionLayer的“函数式”编程方法会更容易。目前，FunctionLayer仅支持Wolfram语言中可用的结构子集——尽管它已经包括许多标准的数组和函数编程操作，并且将来还会增加更多。

FunctionLayer的一个重要功能是，它产生的神经网络将与其他任何神经网络一样高效，并且可以在GPU等上运行。但是，对于FunctionLayer尚不支持的Wolfram语言构造，您可以怎么做？在版本12.2中，我们添加了另一个新的实验函数CompiledLayer，该函数扩展了可以有效处理的Wolfram语言代码的范围。

也许值得解释一下内部发生的事情。我们的主要神经网络框架本质上是一个符号层，用于组织事物以优化底层实现（当前使用MXNet）。FunctionLayer有效地将某些Wolfram语言构造直接转换为MXNet。CompiledLayer会将Wolfram语言转换为LLVM，然后转换为机器代码，并将其插入MXNet中的执行过程。CompiledLayer利用了新的Wolfram语言编译器及其广泛的类型推断和类型声明机制。

好的，假设我们在Wolfram语言框架中建立了一个宏伟的神经网络。一切都已设置好，因此该网络可以立即用于Wolfram语言的所有超级函数（Classify，FeatureSpacePlot，AnomalyDetection，FindClusters等）。但是，如果要在外部环境中“独立”使用网络怎么办？在版本12.2中，我们引入了能够以最近开发的ONNX标准表示形式导出几乎所有网络的功能。

一旦拥有ONNX形式的网络，就可以使用外部工具的整个生态系统将其部署在各种各样的环境中。一个著名的例子（现在是一个相当简化的过程）是采用完整的Wolfram语言创建的神经网络，并在iPhone的CoreML中运行它，以便例如可以将其直接包含在移动应用程序中。