SYNOPSYS光学设计软件|ASAP光学设计软件|SOLIDWORKS 三维建模设计软件|RP Fiber Power仿真设计软件|武汉墨光科技有限公司

技术资源

接近海森堡极限的实验光学相位测量

精确测量是科学和技术的核心，如何使探测系统达到最精度能是一个重要的基本问题。由于物理源基本是是量子化的，因此量子物理学决定了可以实现的最终精度。相关量子源，例如纠缠状态，在测量中可以提供比独立使用量子系统更强的精度。量子增强光学相位估计有望改进目前使用干涉测量的所有测量精度。这种光学量子计量可以分为两个不同的任务。在相位检测中，一个非常具体的情况是确定关于已经众所周知的相位中的小偏差。原则上，使用最大路径纠缠的NOON状态可以为该任务提供最佳灵敏度。更具挑战性的任务是相位测量，有时称为初始相位测量，目的是在没有关于其值的先验信息的情况下确定未知相位φ。在这种情况下，使用光学相移自适应量子测量，或纠缠自适应量子测量的多次通过方法，已经证明能够超过散粒噪声限制（SNL）。SNL表示通过一定数量光子相移的N个独立样本可实现的最小方差。相位测量方案不限于光学方法：例如，等效技术还使用在由磁场引起的单NV中心叠加态的相移测量上。

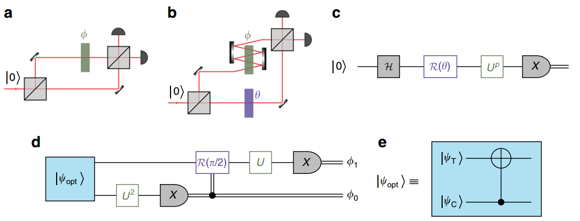
图1 光学相位测量概念。a，用于估计未知相位φ的基本干涉设置；b，高级干涉仪的概念方案，其包括多次（p）通过的相移φ和参考臂中可控相位θ的；c，b中所示干涉仪的量子电路表示；d，用于N = 3源的海森堡极限干涉相位估计的量子电路。原则上，该协议可扩展到更高的N；e，用于制备最佳状态的量子电路。

一开始光学相位测量的任务就是完全估计未知的相位，在具有开销因子的情况下，已经通过实验证明其精度超出了SNL，甚至达到了最终界限，海森堡极限（HL）。然而，现有的方法甚至在原理上都不能达到最佳可能的精度，从而精确地饱和HL。近日，格里菲斯大学的科学家演示了一种解决量子计量学的一个悬而未决的基本问题的技术：如何在最佳的HL上测量相位？它们提出了一个具体的方法来实现以前在理论上提出的概念方案，并实施实验。与之前的光子初始相位估计实验一样，格里菲斯大学的科学家在检测资源方面描述了实验的实施质量——它依靠概率状态制备和测量方案，在精度计算时只考虑成功的符合检测。因此，科学家证明了该方案的原理，将来可以扩展到删除后选择性要素。光子光学相位测量的基本概念如图1a所示。更通用的协议可能包括更复杂的技术：干涉仪路径中光的量子态、对一些光子相移进行多次相干采样的概率和检测策略。

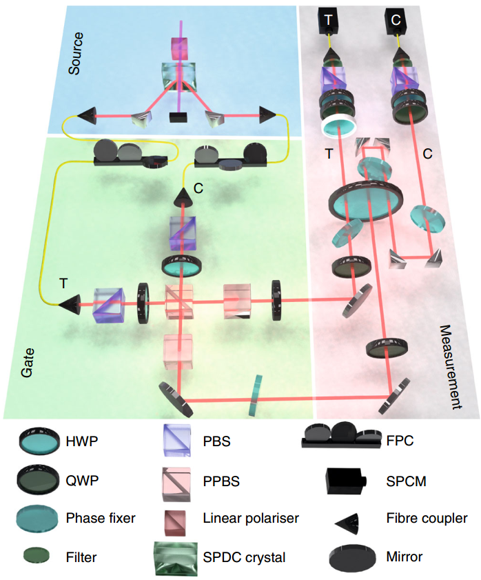
图2 实验装置的示意图。蓝色背景：I型自发参数下转换（SPDC）生成820 nm单光子。绿色背景：纠缠门。

Heisenberg极限干涉相位估计算法（HPEA）如图1d所示，科学家演示了利用三种技术的组合来实现真正的达到HL相位测量的方案：纠缠、相移的多重采样和自适应测量。如图2所示，使用正交的左右圆偏振光而不是路径来形成干涉仪的两个臂。在图2中由灰色背景突出显示偏振干涉仪，使用一个大的半波板（HWP）来实现臂之间的未知相移，模式C通过这个未知相位两次。因此，对于一个成功的符合检测，光子通过次数是N=3。另一个HWP（图2中带有白色边框）用作模式T上的参考相移θ，以便实现检测方案。每次运行使用固定波片，并且基于来自标记为C的检测器结果对数据进行选择性分类，非确定性地实施了前馈步骤。虽然这种方法不足以从一次测量中进行估算，但它是一种准确的方法来表征该方案在多次重复中的表现。

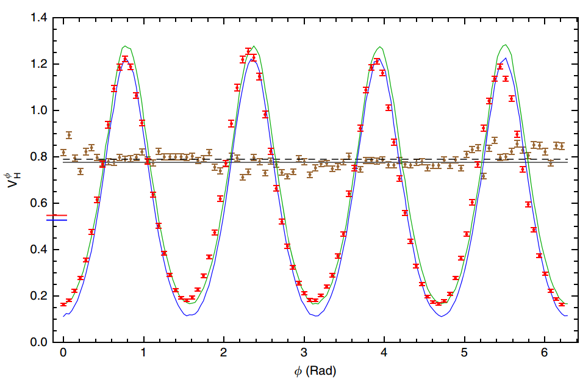
图3 N = 3时海森堡极限相位估计。红点表示实验测量的方差Holevo方差作为φ的函数。切割左轴的红色水平线段显示最佳协议Holevo方差为0.5497±0.0007，蓝线段显示海森堡极限。蓝色和绿色曲线分别代表理想最佳态和实验制备态的数值模拟方差结果。棕色点代表干涉测量的Holevo方差散粒噪声极限。黑色虚线表示相同测量的Holevo方差，测量值为0.7870±0.0007。灰色实线表示SNL。

在估计相位φ时，使用条件Holevo方差来表征HPEA算法的性能，如图3所示。当φ= 0，π/2，π和3π/2时，该协议表现最佳，对应于四个可能的检测结果中只有一个出现的情况：dd，ad，da和aa分别如图4所示。d（a）表示X基态下的对角（反对角）偏振态。由于在不使用任何φ的先验知识的情况下要评估从初始相位估计的精度，因此，通过计算无条件的Holevo方差来擦除任何初始相位信息。最终发现其值为0.5497±0.0007，而N = 3资源量时，海森堡极限约为0.5278。从图3的仿真结果中可以看出，实验结果和理论之间的这种4%的差异可归因于所制备的纠缠态相对于最佳态的非单位保真度，表明了协议性能与制备态质量之间的强相关性。为了进行对比，文章还使用了三个独立的光子执行标准量子干涉测量。计算该测量的Holevo方差是0.7870±0.0007，其接近对于具有N = 3源的SNL=0.7778的理论值。相关内容以《Experimental optical phase measurement approaching the exact Heisenberg limit》为题，发表在《Nature Communications》杂志上。

图4 测量结果的概率分布。