解决方案
2017 年普通高等学校招生全国统一考试
数 学(理)(北京卷)
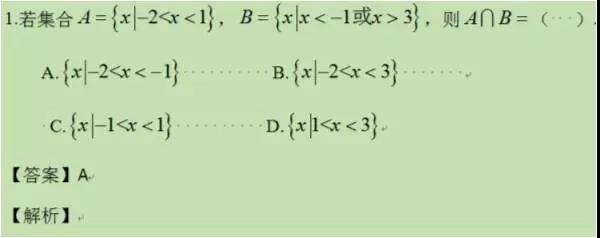
In[1]:= Reduce[{-2
Out[1]= -2
In[2]:= z=(1-I) (a+I); Reduce[{Re[z]<0,Im[z]>0,a\[Element]Reals},a]
Out[3]= a<-1
In[4]:= k=0;s=1;While[k<3,k=k+1;s=(s+1)/s]; s
Out[4]= 5/3
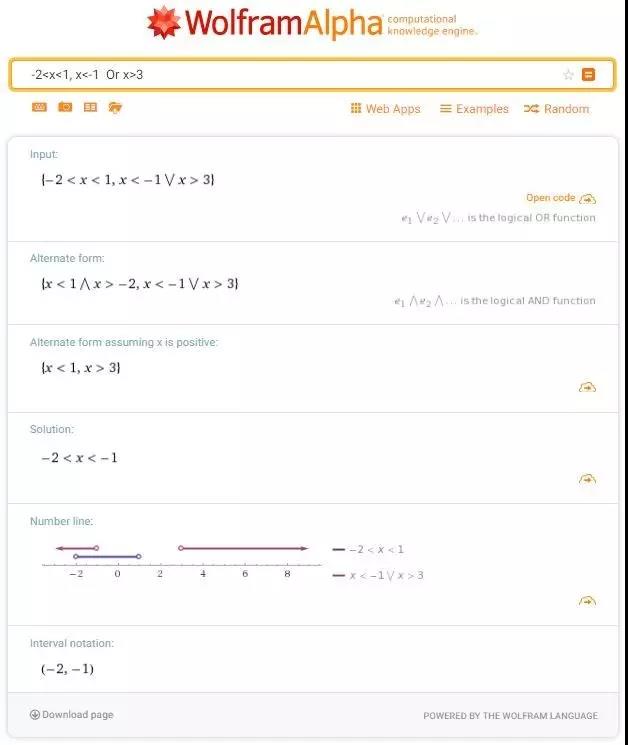
In[5]:= MaxValue[{x+2 y,x<=3,x+y>=2,y<=x},{x,y},Reals]
Out[5]= 9
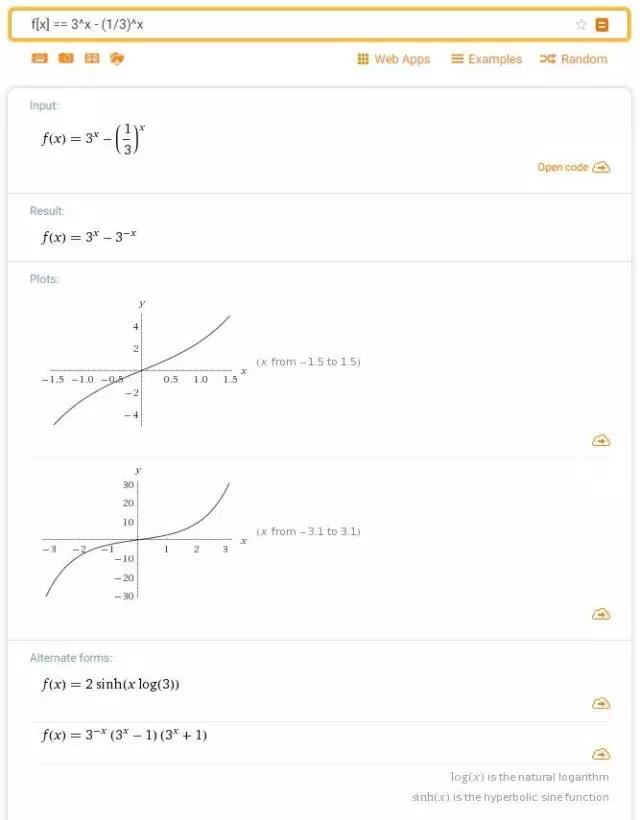
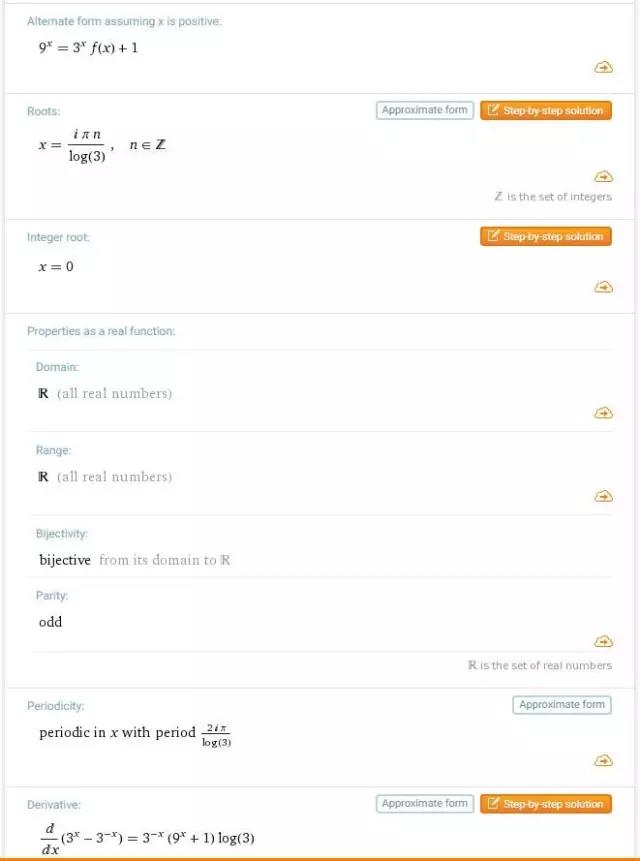
In[6]:= f[x_] = 3^x- (1/3)^x; FullSimplify [{f[-x] == -f[x], f[-x] == f[x]}]
Out[7]= {True,Sinh[x Log[3]]==0}
由计算可知, f(x) 是奇函数.
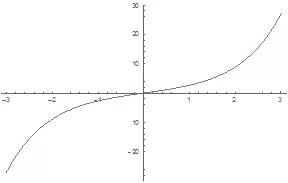
In[8]:= Plot [f[x], {x, -3,3}]
Out[8]=
由图可知,f(x) 是增函数.
神器的分步解答,一定不能错过哦!
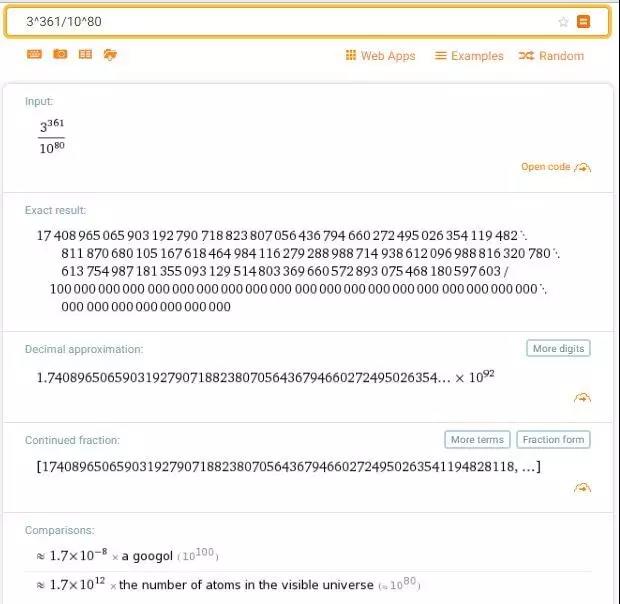
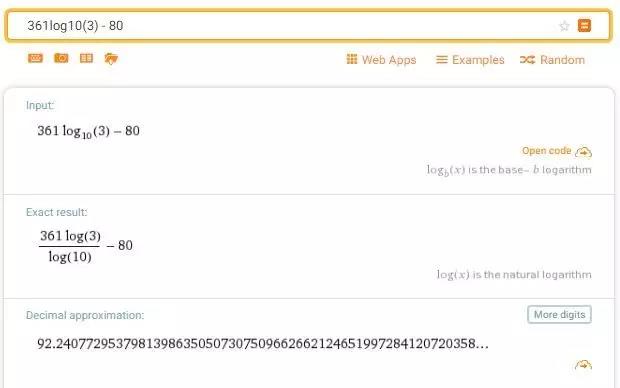
In[13]:= m=3^361;n=10^80;N[m/n]
Out[13]= 1.7409*10^92
In[14]:= Clear[m];
In[15]:= Reduce[Sqrt[1 + m]/1==Sqrt[3], m]
Out[15]= m==2
In[16]:= ClearAll[a1,b1,a4,b4, q, d]
In[17]:= a1=b1=-1; a4=b4=8; d=1/3 (a4-a1); q=Surd[b4/b1, 3];(a1+d)/(b1*q)
Out[21]= 1
In[22]:= A = {x,y}; P ={1,0};
In[23]:= Sqrt@MinValue[{(x-1)^2+y^2,x^2+y^2-2x-4y+4==0},{x,y}]
Out[23]= 1
In[24]:= Solve[{Sin[x] == 1/3, Cos[x-y] == m , 0 < x < y< \[Pi], x+y == \[Pi]}, m, {x,y}, Reals]
Out[24]= {{m->-(7/9)}}
In[19]:= FindInstance[! Implies[a > b > c, a + b > c], {a, b, c}]
Out[19]= {{a -> -2, b -> -3, c -> -4}}
(1)
In[20]:= A = \[Pi]/3; c = 3/7 a;
jC = jC /. Solve[{c/Sin[jC] == a/Sin[A], 0 < jC < \[Pi]/2}, jC][[1, 1]];
Sin[jC]
Out[22]= (3 Sqrt[3])/14
(2)
In[23]:= a = 7; B = \[Pi] - A - jC;
In[24]:= 1/2 a c Sin[B] // FullSimplify
Out[24]= 6 Sqrt[3]
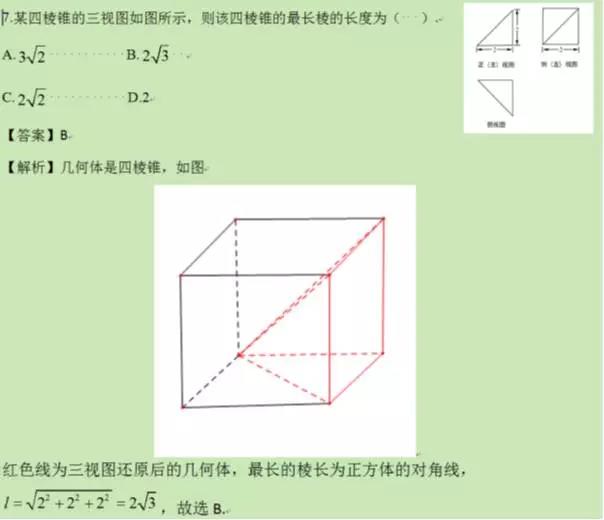
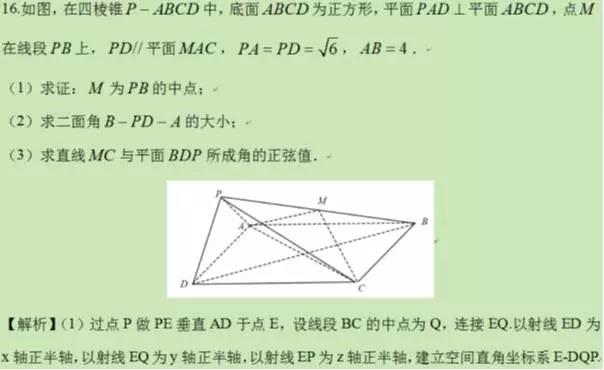
In[25]:= A = {-2, 0, 0}; B = {-2, 4, 0};
dC = {2, 4, 0}; dD = {2, 0, 0};
P = {0, 0, Sqrt[2]};
PB = B - P;
M := P + t PB;
MA := A - M;
MC := dC - M;
PD = dD - P;
Solve[PD.(MA \[Cross] MC) == 0, t , Reals]
Out[31]= {{t -> 1/2}}
由以上计算可知,M 为 PB 的中点. (2)
In[32]:= DA = A - dD; \[Pi] - VectorAngle[PD \[Cross] DA, PB \[Cross] PD]
Out[32]= \[Pi]/3
(3)
In[33]:= Sin[VectorAngle[MC /. t -> 1/2, PB \[Cross] PD] - \[Pi]/2] // Simplify
Out[33]= (2 Sqrt[2/3])/3
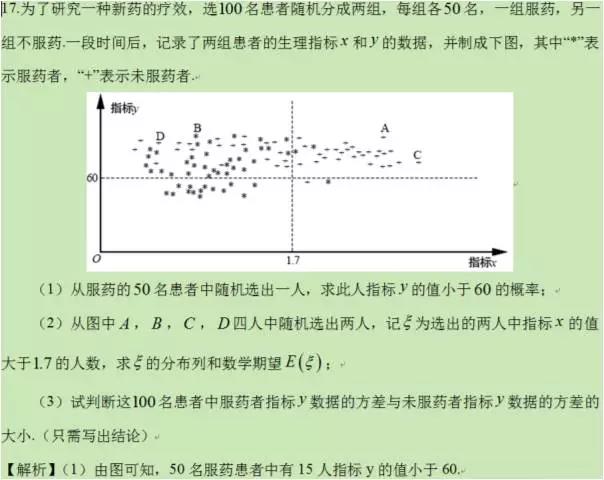
(3)服药者指标 y 数据的方差大于未服药者指标 y 数据的方差.
【解析】(1)
In[44]:= f[x_] = E^x Cos[x] - x;
df[x_] = D[f[x], x];y - f[0] == df[0]*x
Out[45]= -1 + y == 0
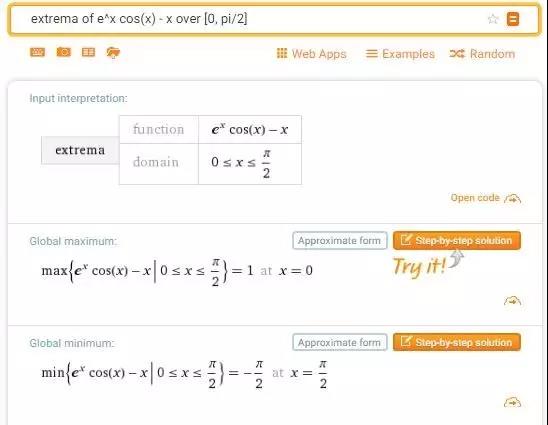
【解析】(2)
In[46]:= FunctionRange[{f[x], 0 \[LessSlantEqual] x \[LessSlantEqual] \[Pi]/2}, x , y]
Out[46]= -(\[Pi]/2) <= y <= 1
In[50]:= ClearAll[a, b, c];
In[51]:= a[n_] := n; b[n_] := 2 n - 1;
c[n_] := c[n] = Max@Table[b[i] - a[i]*n, {i, n}]{c[1], c[2], c[3]}
Out[53]= {0, -1, -2}










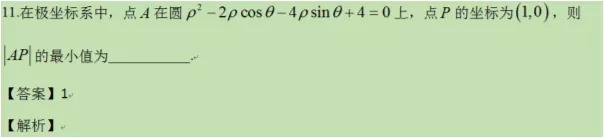










ASAP/APEX技术交流群 373021576
SYNOPSYS光学设计与优化交流群 965722997
RP激光软件交流群 302099202
武汉墨光科技有限公司
友情链接
Copyright © 2012-2021 武汉墨光科技有限公司版权所有
许可证:鄂ICP备17024342号-1

